第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
7. 如图是一个正方体的表面展开图,已知正方体相对两个面上的数值相同,且不相对两个面上的数值不相同,则“★”面上的数为(
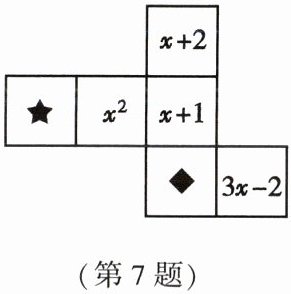
A.1
B.1 或 2
C.2
D.2 或 3
C
)
A.1
B.1 或 2
C.2
D.2 或 3
答案:
7.C
8. 已知 $ a $,$ b $,$ c $ 是 $ \triangle ABC $ 三边的长,则方程 $ ax^{2}+(b + c)x+\frac{a}{4}=0 $ 的根的情况为(
A.没有实数根
B.有两个相等的正实数根
C.有两个不相等的负实数根
D.有两个异号的实数根
C
)A.没有实数根
B.有两个相等的正实数根
C.有两个不相等的负实数根
D.有两个异号的实数根
答案:
8.C
9. 等腰三角形的一边长是 3,另两边的长是关于 $ x $ 的方程 $ x^{2}-4x + k = 0 $ 的两个根,则 $ k $ 的值为(
A.3
B.4
C.3 或 4
D.7
C
)A.3
B.4
C.3 或 4
D.7
答案:
9.C
10. 在平面直角坐标系中,若直线 $ y=-x + m $ 不经过第一象限,则关于 $ x $ 的方程 $ mx^{2}+x + 1 = 0 $ 的实数根的个数为(
A.0
B.1
C.2
D.1 或 2
D
)A.0
B.1
C.2
D.1 或 2
答案:
10.D
11. (2022·连云港)若关于 $ x $ 的一元二次方程 $ mx^{2}+nx - 1 = 0(m\neq0) $ 的一个根是 $ x = 1 $,则 $ m + n $ 的值是
1
。
答案:
11.1
12. 关于 $ x $ 的一元二次方程 $ (k + 2)x^{2}+6x + k^{2}+k - 2 = 0 $ 有一个根是 0,则 $ k $ 的值是
1
。
答案:
12.1
13. 王叔叔从市场上买一块长 80cm、宽 70cm 的矩形铁皮,准备制作一个工具箱。如图,他将矩形铁皮的四个角各剪掉一个边长为 $ xcm $ 的正方形后,剩余的部分刚好能围成一个底面积为 $ 3000cm^{2} $ 的无盖长方体工具箱。根据题意可列方程为
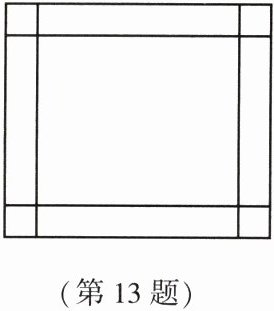
(80-2x)(70-2x)=3000
。
答案:
13.(80-2x)(70-2x)=3000
14. 一元二次方程 $ x^{2}-3x - 1 = 0 $ 与 $ x^{2}-x + 3 = 0 $ 的所有实数根的和等于
3
。
答案:
14.3
15. 某公司今年 7 月的营业额为 2500 万元,按计划第三季度的总营业额要达到 9100 万元,设该公司 8,9 两月的营业额的月平均增长率为 $ x $。根据题意列方程为
2500+2500(1+x)+2500(1+x)^2=9100
。
答案:
$15.2500+2500(1+x)+2500(1+x)^2=9100$
16. (8 分)用指定的方法解下列方程:
(1)$ x(x - 6)=6 $(用配方法);
(2)$ 4x^{2}+2x - 1 = 0 $(用公式法)。
(1)$ x(x - 6)=6 $(用配方法);
(2)$ 4x^{2}+2x - 1 = 0 $(用公式法)。
答案:
16.
(1)原方程变形为$x^2-6x=6,$
则$x^2-6x+9=6+9,$即$(x-3)^2=15,$
章 一元二次方程
$x-3=\pm\sqrt{15},$
$x_1=3+\sqrt{15},x_2=3-\sqrt{15}。$
(2)由题意,知$a=4,b=2,c=-1,b^2-4ac=2^2-4×$
4×(-1)=20>0,
$x=\frac{-2\pm2\sqrt{5}}{8},$
$x_1=\frac{-1+\sqrt{5}}{4},x_2=\frac{-1-\sqrt{5}}{4}$
(1)原方程变形为$x^2-6x=6,$
则$x^2-6x+9=6+9,$即$(x-3)^2=15,$
章 一元二次方程
$x-3=\pm\sqrt{15},$
$x_1=3+\sqrt{15},x_2=3-\sqrt{15}。$
(2)由题意,知$a=4,b=2,c=-1,b^2-4ac=2^2-4×$
4×(-1)=20>0,
$x=\frac{-2\pm2\sqrt{5}}{8},$
$x_1=\frac{-1+\sqrt{5}}{4},x_2=\frac{-1-\sqrt{5}}{4}$
查看更多完整答案,请扫码查看


