《2025年基础训练大象出版社九年级数学全一册北师大版》

16. (8分)计算:$|-1|-\frac{1}{2}\sqrt{8}-(5-\pi)^{0}+4\sin45^{\circ}$.

答案： 16.|-1| - $\frac{1}{2}$√8 - (5 - π)° + 4sin45°
= 1 - $\frac{1}{2}$×2√2 - 1 + 4×$\frac{\sqrt{2}}{2}$　　　　　　　　　　　　6分
= √2.　　　　　　　　　　　　　　　　　　　　8分

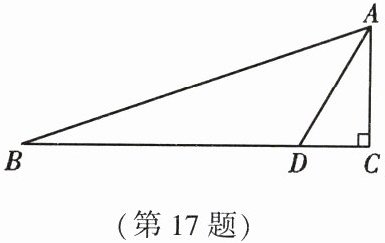
17. (9分)如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ},AC = \sqrt{3}$. $D$为$BC$边上一点,且$BD = 2AD,\angle ADC = 60^{\circ}$,求$\triangle ABC$的周长(结果保留根号).

答案： 17.
∵　　∠C = 90°,∠ADC = 60°,
∴　　CD = ACtan30° = 1.　　　　　　　　　　　　2分
∴　AD = √(AC² + CD²) = √(1² + (√3)²) = 2.　　　　4分
∴　　BD = 2AD = 4.　　　　　　　　　　　　　　　6分
∴　AB = √(AC² + BC²) = 2√7.　　　　　　　　　　8分
∴　　△ABC的周长 = AB + AC + BC = 5 + 2√7 + √3
　　　　　　　　　　　　　　　　　　　　9分

18. (9分)已知$y = (k + 2)x^{k^{2}+k - 4}+2$是二次函数,且当$x ＜ 0$时,$y$随$x$的增大而增大.
(1)求$k$的值;
(2)求顶点坐标和对称轴.

答案： 18.
(1)根据题意,得k² + k - 4 = 2,解得k1 = -3,k2 = 2.
　　　　　　　　　　　　　　　　　　　　2分
当k = -3时,函数的解析式为y = -x² + 2,当x＜0时,y随x的增大而增大;　　　　　　　　　　　　3分
当k = 2时,函数的解析式为y = 4x² + 2,当x＜0时,y随x的增大而减小.　　　　　　　　　　　　　　　4分
∴　　k = -3.　　　　　　　　　　　　　　　　　　5分
(2)y = -x² + 2的顶点坐标为(0,2),　　　　　　　7分
对称轴为y轴.　　　　　　　　　　　　　　　　9分