《2025年基础训练大象出版社九年级数学全一册北师大版》

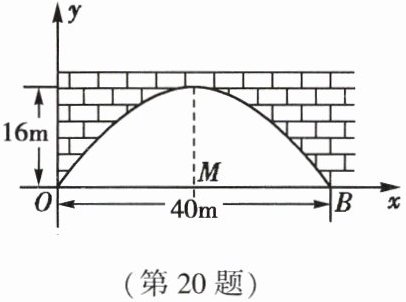
20. （9 分）有一个抛物线状的拱形桥，这个桥拱的最大高度为$16m$，跨度为$40m$，现把它放在如图所示的平面直角坐标系中，若要在离跨度中心点$M$$5m$处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？

答案： 20.由题意,知抛物线的顶点坐标为(20,16),点B的坐标为(40,0)，
∴　　可设抛物线的关系式为y=a(x−20)²+16.
∵　　点B(40,0)在抛物线上，
∴　0=a(40−20)²+16.
∴　　a=−$\frac{1}{25}$.
∴　　y=−$\frac{1}{25}$(x−20)²+16.
∵　　竖立柱的点为(15,0)或(25,0),
∴　　当x=15 时,y=−$\frac{1}{25}$×(15−20)²+16=15;当x=25时,y=−$\frac{1}{25}$×(25−20)²+16=15.
∴　　铁柱应取15m.

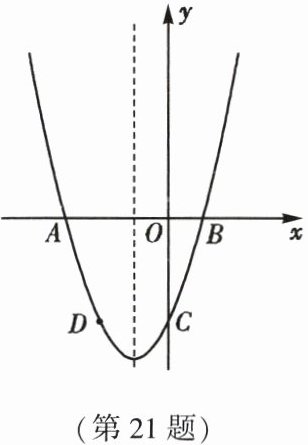
21. （10 分）如图，已知二次函数$y = x^2 + bx + c$的图象与$x$轴交于$A$，$B$两点，其中点$A$的坐标为$(-3, 0)$，与$y$轴交于点$C$，点$D(-2, -3)$在抛物线上。
（1）求抛物线的表达式；
（2）若抛物线上有一动点$P$，使$\triangle ABP$的面积为 6，求点$P$的坐标。

答案： 21.
(1)
∵　　二次函数y=x²+bx+c的图象经过A(−3,0),D(−2,−3),
∴　　$\begin{cases}9 - 3b + c = 0,\\4 - 2b + c = -3,\end{cases}$解得$\begin{cases}b = 2,\\c = -3.\end{cases}$
∴　　抛物线的表达式为y=x²+2x−3.
(2)设点P的坐标为(m,m²+2m−3).
令y=0,则x²+2x−3=0,
解得x₁=−3,x₂=1,
∴　点B的坐标为(1,0)，
∴　AB=4.
∵　S△ABP=6,
∴　　$\frac{1}{2}$×4×|m²+2m−3|=6,
∴　　m²+2m=0,或m²+2m−6=0,
解得m₁=0,m₂=−2,或m₃=−1+$\sqrt{7}$,m₄=−1−$\sqrt{7}$,
∴　　点P的坐标为(0,−3)或(−2,−3)或(−1+$\sqrt{7}$,3)或(−1−$\sqrt{7}$,3).

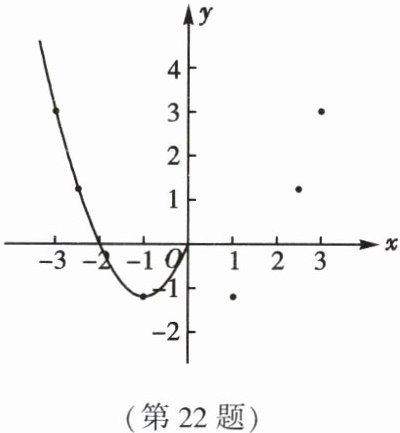
22. (10 分)某班“数学兴趣小组”对函数$y = x^2 - 2|x|$的图象和性质进行了探究，探究过程如下，请解答相应问题。
(1)自变量$x$的取值范围是全体实数，$x$与$y$的几组对应值列表如下：
其中，$m =$0。
(2)根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分。
(3)观察函数图象，写出两条函数的性质。
(4)进一步探究函数图象发现：
①函数图象与$x$轴有3个交点，所以对应的方程$x^2 - 2|x| = 0$有3个实数根；
②方程$x^2 - 2|x| = 2$有2个实数根；
③关于$x$的方程$x^2 - 2|x| = a$有 4 个实数根时，$a$的取值范围是−1＜a＜0。

答案： 22.
(1)0　
(2)略.　　
(3)略.　　[提示]可从函数的最值、增减性、图象的对称性等方面阐述.答案不唯一，合理即可.　　
(4)①3　3　②2　③−1＜a＜0