《2025年基础训练大象出版社九年级数学全一册北师大版》

18. （9 分）已知一次函数$y = ax + b$的图象上有两点$A$，$B$，它们的横坐标分别是 3，$-1$，二次函数$y = \frac{1}{3}x^2$的图象经过$A$，$B$两点。
（1）请求出一次函数的解析式；
（2）设二次函数的顶点为$C$，求$\triangle ABC$的面积。

答案： 18.
(1)由题意,知A(3,3),B(−1,$\frac{1}{3}$),可求出一次函数的解析式为y=$\frac{2}{3}x+1$.　　
(2)C(0,0),S△ABC=2.

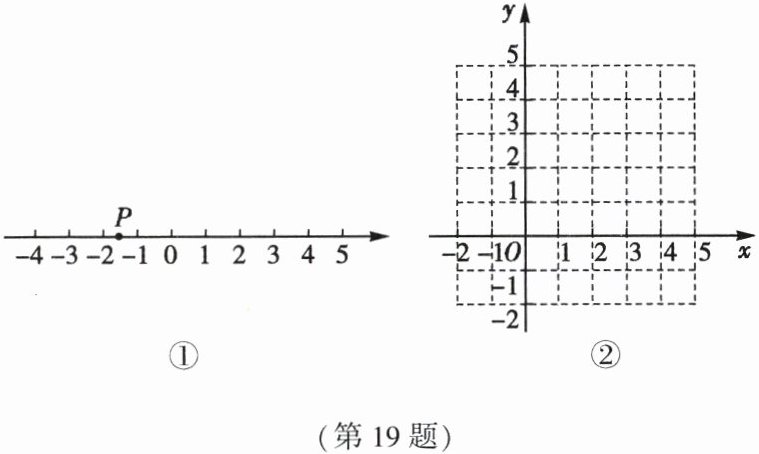
19. (9 分)如图①，$P$为数轴上任意一点，其对应的实数为$x$，点$P$的位置用$P(x, 0)$表示。点$P$由左到右、从负半轴向正半轴运动时，点$P$到原点$O$的距离先变小再变大，当点$P$的位置确定时，点$P$到原点的距离也唯一确定。
(1)设点$P(x, 0)$到点$A(2, 0)$的距离为$d$，可发现$d$是$x$的函数。当$x =$2时，$d$取最

小

值。
(2)设点$P(x, 0)$到点$O(0, 0)$，$A(2, 0)$的距离之和为$y$。
①在图②所示的平面直角坐标系中画出表示变量$y$和$x$之间关系的图象。
②$y$是不是$x$的函数？为什么？
③当$y ＜ 5$时，$x$的取值范围是−$\frac{3}{2}$＜x＜$\frac{7}{2}$。

答案：
19.
(1)2　
(2)①由题意,当x=1时,y=1+1=2;
　当x=2时,y=2+0=2;
　当x=3时,y=3+1=4;
　当x=−1时,y=4;…
　图象如图所示.
　　　　　　
　②y是x的函数,因为对于x的每一个确定的值,y都有唯一的值与其对应.
③−$\frac{3}{2}$＜x＜$\frac{7}{2}$