《2025年基础训练大象出版社九年级数学全一册北师大版》

1. 下列函数，$y$是关于$x$的二次函数的是(C)

A.$y = ax^2 + bx + c$
B.$y = \frac{1}{x^2 + 1}$
C.$y = x(x + 1)$
D.$y = (x + 2)^2 - x^2$

答案： 1.C

2. 给出下列四个函数：①$y = -2x$；②$y = 2x - 1$；③$y = \frac{3}{x}(x ＞ 0)$；④$y = -x^2 + 3(x ＞ 0)$。其中$y$随$x$的增大而减小的函数有(A)

A.3 个
B.2 个
C.1 个
D.0 个

答案： 2.A

3. 把抛物线$y = -2x^2 + 4x + 1$的图象向左平移 2 个单位长度，再向上平移 3 个单位长度，所得的抛物线的函数关系式是(C)

A.$y = -2(x - 1)^2 + 6$
B.$y = -2(x - 1)^2 - 6$
C.$y = -2(x + 1)^2 + 6$
D.$y = -2(x + 1)^2 - 6$

答案： 3.C

4. 若所求的二次函数图象与抛物线$y = 2x^2 - 4x - 1$有相同的顶点，并且在对称轴的左侧，$y$随$x$的增大而增大，在对称轴的右侧，$y$随$x$的增大而减小，则所求的二次函数表达式为(D)

A.$y = -x^2 + 2x + 4$
B.$y = -ax^2 - 2ax - 3(a ＞ 0)$
C.$y = -2x^2 - 4x - 5$
D.$y = ax^2 - 2ax + a - 3(a ＜ 0)$

答案： 4.D

5. 函数$y = ax^2 + bx + c$的图象如图所示，那么关于$x$的方程$ax^2 + bx + c - 3 = 0$的根的情况是(C)

A.有两个不相等的实数根
B.有两个异号的实数根
C.有两个相等的实数根
D.无实数根

答案： 5.C

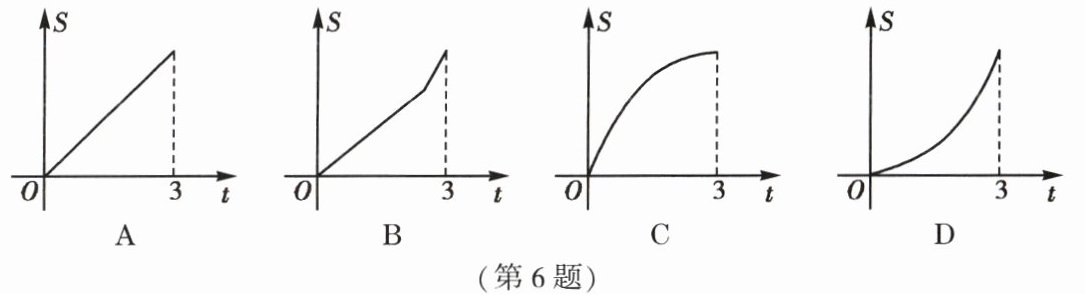
6. 如图，在$Rt\triangle AOB$中，$AB \perp OB$，且$AB = OB = 3$，设直线$x = t$截此三角形所得阴影部分的面积为$S$，则$S$与$t$之间的函数关系的图象为下列选项中的(D)

答案： 6.D