第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
23. (11 分)阅读理解学习。
在学习“直角三角形的边角关系”这一章时,小迪同学勤学好问,在课外学习活动中,探究发现三角形的面积、边、角之间存在一定的数量关系,下面是她的学习笔记。请仔细阅读并完成相应的任务。
【阅读材料】在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 的对边分别记为 $ a $,$ b $,$ c $,$ \triangle ABC $ 的面积记为 $ S_{\triangle ABC} $,过点 $ A $ 作 $ AD \perp BC $,垂足为 $ D $。$ \because \sin B = \frac{AD}{AB} $,$ \therefore AD = AB · \sin B $。
$ \therefore S_{\triangle ABC} = \frac{1}{2}BC · AD = \frac{1}{2}BC · AB · \sin B = \frac{1}{2}a · c · \sin B $。
同理可得 $ S_{\triangle ABC} = \frac{1}{2}b · c · \sin A $,$ S_{\triangle ABC} = \frac{1}{2}a · b · \sin C $。
$ \therefore S_{\triangle ABC} = \frac{1}{2}b · c · \sin A = \frac{1}{2}a · c · \sin B = \frac{1}{2}a · b · \sin C $。……①
由以上推理得结论①:三角形的面积等于两边及其夹角正弦积的一半。
又 $ abc \neq 0 $,将等式 $ \frac{1}{2}b · c · \sin A = \frac{1}{2}a · c · \sin B = \frac{1}{2}a · b · \sin C $ 两边同除以 $ \frac{1}{2}abc $,得 $ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} $,即 $ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $。……②
由以上推理得结论②:在一个三角形中,各边和它所对角的正弦的比值相等。
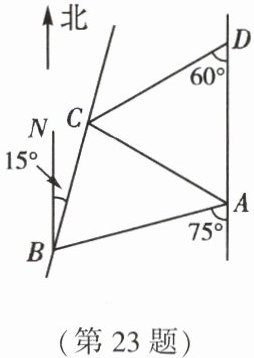
【理解应用】如图,甲船以 $ 24\sqrt{3} $ 海里/时的速度向正北方向航行,当甲船位于 $ A $ 处时,乙船位于甲船的南偏西 $ 75^{\circ} $ 方向的 $ B $ 处,且乙船从 $ B $ 处沿北偏东 $ 15^{\circ} $ 方向匀速直线航行,当甲船航行 $ 20 $ 分钟到达 $ D $ 处时,乙船航行到甲船的南偏西 $ 60^{\circ} $ 方向的 $ C $ 处,两船相距 $ 8\sqrt{3} $ 海里。
(1)求 $ \triangle ADC $ 的面积;
(2)求乙船航行的路程为多少海里。(结果保留根号)
在学习“直角三角形的边角关系”这一章时,小迪同学勤学好问,在课外学习活动中,探究发现三角形的面积、边、角之间存在一定的数量关系,下面是她的学习笔记。请仔细阅读并完成相应的任务。
【阅读材料】在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 的对边分别记为 $ a $,$ b $,$ c $,$ \triangle ABC $ 的面积记为 $ S_{\triangle ABC} $,过点 $ A $ 作 $ AD \perp BC $,垂足为 $ D $。$ \because \sin B = \frac{AD}{AB} $,$ \therefore AD = AB · \sin B $。
$ \therefore S_{\triangle ABC} = \frac{1}{2}BC · AD = \frac{1}{2}BC · AB · \sin B = \frac{1}{2}a · c · \sin B $。
同理可得 $ S_{\triangle ABC} = \frac{1}{2}b · c · \sin A $,$ S_{\triangle ABC} = \frac{1}{2}a · b · \sin C $。
$ \therefore S_{\triangle ABC} = \frac{1}{2}b · c · \sin A = \frac{1}{2}a · c · \sin B = \frac{1}{2}a · b · \sin C $。……①
由以上推理得结论①:三角形的面积等于两边及其夹角正弦积的一半。
又 $ abc \neq 0 $,将等式 $ \frac{1}{2}b · c · \sin A = \frac{1}{2}a · c · \sin B = \frac{1}{2}a · b · \sin C $ 两边同除以 $ \frac{1}{2}abc $,得 $ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} $,即 $ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $。……②
由以上推理得结论②:在一个三角形中,各边和它所对角的正弦的比值相等。
【理解应用】如图,甲船以 $ 24\sqrt{3} $ 海里/时的速度向正北方向航行,当甲船位于 $ A $ 处时,乙船位于甲船的南偏西 $ 75^{\circ} $ 方向的 $ B $ 处,且乙船从 $ B $ 处沿北偏东 $ 15^{\circ} $ 方向匀速直线航行,当甲船航行 $ 20 $ 分钟到达 $ D $ 处时,乙船航行到甲船的南偏西 $ 60^{\circ} $ 方向的 $ C $ 处,两船相距 $ 8\sqrt{3} $ 海里。
(1)求 $ \triangle ADC $ 的面积;
(2)求乙船航行的路程为多少海里。(结果保留根号)

答案:
23.
(1)由题意知,$\angle ADC = 60°$,$DC = 8\sqrt{3}$海里,$AD = 24\sqrt{3} × \frac{20}{60} = 8\sqrt{3}$(海里),
由材料中结论①知,$S_{\triangle ADC} = \frac{1}{2}DC · AD · \sin \angle ADC = \frac{1}{2} × 8\sqrt{3} × 8\sqrt{3} × \sin60° = \frac{1}{2} × 8\sqrt{3} × 8\sqrt{3} × \frac{\sqrt{3}}{2} = 48\sqrt{3}$(平方海里),
所以$\triangle ADC$的面积为$48\sqrt{3}$平方海里.
(2)由
(1)知,$DC = AD$,$\angle ADC = 60°$,$\therefore$ $\triangle ACD$是等边三角形,

$\therefore$ $\angle DAC = 60°$,$AC = AD = 8\sqrt{3}$海里.
又$\angle BAM = 75°$,$\therefore$ $\angle BAC = 180° - 75° - 60° = 45°$.
由题意知,$\angle NBC = 15°$,$\angle NBA = 75°$,$\therefore$ $\angle ABC = 75° - 15° = 60°$.
在$\triangle ABC$中,由材料中结论②,得$\frac{AC}{\sin \angle ABC} = \frac{BC}{\sin \angle BAC}$,$\therefore$ $BC = \frac{AC · \sin \angle BAC}{\sin \angle ABC} = \frac{8\sqrt{3} × \sin45°}{\sin60°} = \frac{8\sqrt{3} × \frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = 8\sqrt{2}$(海里),$\therefore$ 乙船航行的路程为$8\sqrt{2}$海里.
23.
(1)由题意知,$\angle ADC = 60°$,$DC = 8\sqrt{3}$海里,$AD = 24\sqrt{3} × \frac{20}{60} = 8\sqrt{3}$(海里),
由材料中结论①知,$S_{\triangle ADC} = \frac{1}{2}DC · AD · \sin \angle ADC = \frac{1}{2} × 8\sqrt{3} × 8\sqrt{3} × \sin60° = \frac{1}{2} × 8\sqrt{3} × 8\sqrt{3} × \frac{\sqrt{3}}{2} = 48\sqrt{3}$(平方海里),
所以$\triangle ADC$的面积为$48\sqrt{3}$平方海里.
(2)由
(1)知,$DC = AD$,$\angle ADC = 60°$,$\therefore$ $\triangle ACD$是等边三角形,

$\therefore$ $\angle DAC = 60°$,$AC = AD = 8\sqrt{3}$海里.
又$\angle BAM = 75°$,$\therefore$ $\angle BAC = 180° - 75° - 60° = 45°$.
由题意知,$\angle NBC = 15°$,$\angle NBA = 75°$,$\therefore$ $\angle ABC = 75° - 15° = 60°$.
在$\triangle ABC$中,由材料中结论②,得$\frac{AC}{\sin \angle ABC} = \frac{BC}{\sin \angle BAC}$,$\therefore$ $BC = \frac{AC · \sin \angle BAC}{\sin \angle ABC} = \frac{8\sqrt{3} × \sin45°}{\sin60°} = \frac{8\sqrt{3} × \frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = 8\sqrt{2}$(海里),$\therefore$ 乙船航行的路程为$8\sqrt{2}$海里.
查看更多完整答案,请扫码查看


