《2025年基础训练大象出版社九年级数学全一册北师大版》

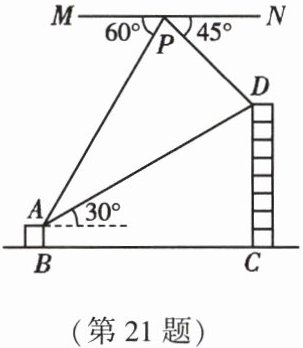
21. (10 分)(2022·海南)无人机在实际生活中应用广泛。如图所示，小明利用无人机测量大楼的高度，无人机在空中 $ P $ 处，测得楼 $ CD $ 楼顶 $ D $ 处的俯角为 $ 45^{\circ} $，测得楼 $ AB $ 楼顶 $ A $ 处的俯角为 $ 60^{\circ} $。已知楼 $ AB $ 和楼 $ CD $ 之间的距离 $ BC $ 为 $ 100 $ 米，楼 $ AB $ 的高度为 $ 10 $ 米，从楼 $ AB $ 的 $ A $ 处测得楼 $ CD $ 的 $ D $ 处的仰角为 $ 30^{\circ} $(点 $ A $，$ B $，$ C $，$ D $，$ P $ 在同一平面内)。
(1)填空：$ \angle APD = $75度，$ \angle ADC = $60度；
(2)求楼 $ CD $ 的高度(结果保留根号)；
(3)求此时无人机距离地面 $ BC $ 的高度。

答案：
21.
(1)75　60
(2)如图，过点$A$作$AE \perp CD$于点$E$.由题意，可得$AE = BC = 100$米，$EC = AB = 10$米.
在$Rt\triangle AED$中，$\angle DAE = 30°$，
$\tan30° = \frac{DE}{AE} = \frac{DE}{100} = \frac{\sqrt{3}}{3}$，
解得$DE = \frac{100\sqrt{3}}{3}$，
$\therefore$ $CD = DE + EC = (\frac{100\sqrt{3}}{3} + 10)$米，
$\therefore$ 楼$CD$的高度为$(\frac{100\sqrt{3}}{3} + 10)$米.

(3)如图，过点$P$作$PG \perp BC$于点$G$，交$AE$于点$F$，则$\angle PFA = \angle AED = 90°$，$FG = AB = 10$米.
$\because$ $MN // AE$，$\therefore$ $\angle PAF = \angle MPA = 60°$.
$\because$ $\angle ADE = 60°$，
$\therefore$ $\angle PAF = \angle ADE$.
$\because$ $\angle DAE = 30°$，
$\therefore$ $\angle PAD = 30°$.
$\because$ $\angle APD = 75°$，
$\therefore$ $\angle ADP = 75°$，
$\therefore$ $\angle ADP = \angle APD$，$\therefore$ $AP = AD$，
$\therefore$ $\triangle APF \cong \triangle DAE(AAS)$，
$\therefore$ $PF = AE = 100$米，
$\therefore$ $PG = PF + FG = 100 + 10 = 110$(米)，
$\therefore$ 此时无人机距离地面$BC$的高度为$110$米.

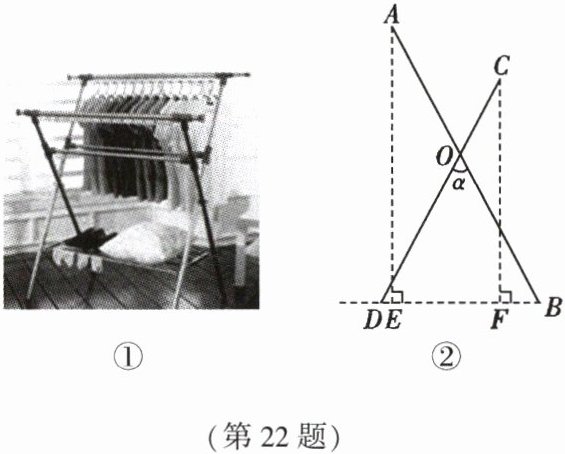
22. （10 分）有一种落地晾衣架如图①所示，其原理是通过改变两根支撑杆夹角 $ \alpha $ 的度数来调整晾杆的高度，图②是晾衣架侧面的平面示意图，$ AB $ 和 $ CD $ 分别是两根长度不等的支撑杆，夹角 $ \angle BOD = \alpha $，$ AO = 70cm $，$ BO = DO = 80cm $，$ CO = 40cm $。
（1）若 $ \alpha = 56^{\circ} $，求点 $ A $ 离地面的高度 $ AE $；
（2）调节 $ \alpha $ 的大小，使点 $ A $ 离地面高度 $ AE = 125cm $，求此时点 $ C $ 离地面的高度 $ CF $。
（参考数据：$ \sin 62^{\circ} = \cos 28^{\circ} \approx 0.88 $，$ \sin 28^{\circ} = \cos 62^{\circ} \approx 0.47 $，$ \tan 62^{\circ} \approx 1.88 $，$ \tan 28^{\circ} \approx 0.53 $）

答案：
22.
(1)如图，过$O$作$OG \perp BD$于点$G$.
$\because$ $AE \perp BD$，
$\therefore$ $OG // AE$，
$\therefore$ $\angle EAB = \angle BOG$.
$\because$ $BO = DO$，
$\therefore$ $OG$平分$\angle BOD$，
$\therefore$ $\angle BOG = \angle DOG = \frac{1}{2}\angle BOD = \frac{1}{2} × 56° = 28°$，

$\therefore$ $\angle EAB = \angle BOG = 28°$.
在$Rt\triangle ABE$中，$AB = AO + BO = 70 + 80 = 150(cm)$，
$\therefore$ $AE = AB · \cos \angle EAB = 150 × \cos 28° \approx 150 × 0.88 = 132(cm)$.
$\therefore$ 点$A$离地面的高度$AE$约为$132cm$.
(2)由
(1)知$\angle EAB = \angle BOG$，$\angle BOG = \angle DOG$.
$\because$ $CF \perp BD$，
$\therefore$ $CF // OG$，
$\therefore$ $\angle DCF = \angle DOG$.
$\therefore$ $\angle BAE = \angle DCF$，
$\because$ $\angle AEB = \angle CFD = 90°$，
$\therefore$ $\triangle AEB \backsim \triangle CFD$，$\therefore$ $\frac{CF}{AE} = \frac{CD}{AB}$，
$\therefore$ $CF = \frac{CD · AE}{AB} = \frac{120 × 125}{150} = 100(cm)$.
$\therefore$ 此时$C$点离地面的高度$CF$为$100cm$.