《2025年基础训练大象出版社九年级数学全一册北师大版》

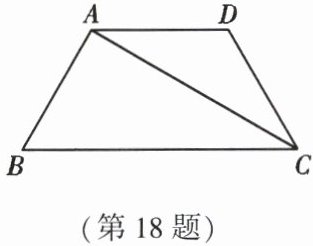
18. （9 分）如图，已知在四边形 $ ABCD $ 中，$ AD // BC $，$ AB = AD = DC = 8 $，$ \angle B = 60^{\circ} $，连接 $ AC $。求 $ \cos \angle ACB $ 的值。

答案： 18.$\because$ 在四边形$ABCD$中，$AD // BC$，$AB = AD = DC = 8$，$\angle B = 60°$，
$\therefore$ 由轴对称的性质知$\angle BCD = 60°$.
$\because$ $\angle ACD = \angle DAC$，$\angle ACB = \angle DAC$，
$\therefore$ $\angle ACD = \angle ACB = 30°$.
$\therefore$ $\cos \angle ACB = \cos 30° = \frac{\sqrt{3}}{2}$.

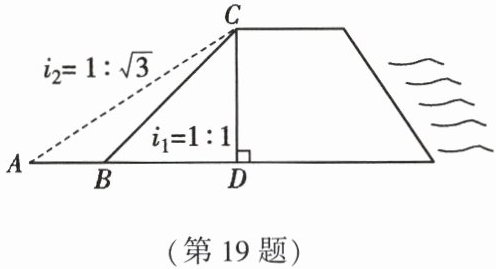
19. （9 分）（2022·郴州）如图是某水库大坝的横截面，坝高 $ CD = 20m $，背水坡 $ BC $ 的坡度为 $ i_1 = 1 : 1 $。为了对水库大坝进行升级加固，降低背水坡的倾斜程度，设计人员准备把背水坡的坡度改为 $ i_2 = 1 : \sqrt{3} $，求背水坡新起点 $ A $ 与原起点 $ B $ 之间的距离。（参考数据：$ \sqrt{2} \approx 1.41 $，$ \sqrt{3} \approx 1.73 $。结果精确到 $ 0.1m $）

答案： 19.在$Rt\triangle BCD$中，
$\because$ $BC$的坡度为$i_1 = 1 : 1$，
$\therefore$ $\frac{CD}{BD} = 1$，
$\therefore$ $CD = BD = 20m$.
在$Rt\triangle ACD$中，
$\because$ $AC$的坡度为$i_2 = 1 : \sqrt{3}$，
$\therefore$ $\frac{CD}{AD} = \frac{1}{\sqrt{3}}$，
$\therefore$ $AD = \sqrt{3}CD = 20\sqrt{3}m$，
$\therefore$ $AB = AD - BD = 20\sqrt{3} - 20 \approx 14.6(m)$，
$\therefore$ 背水坡新起点$A$与原起点$B$之间的距离约为$14.6m$.

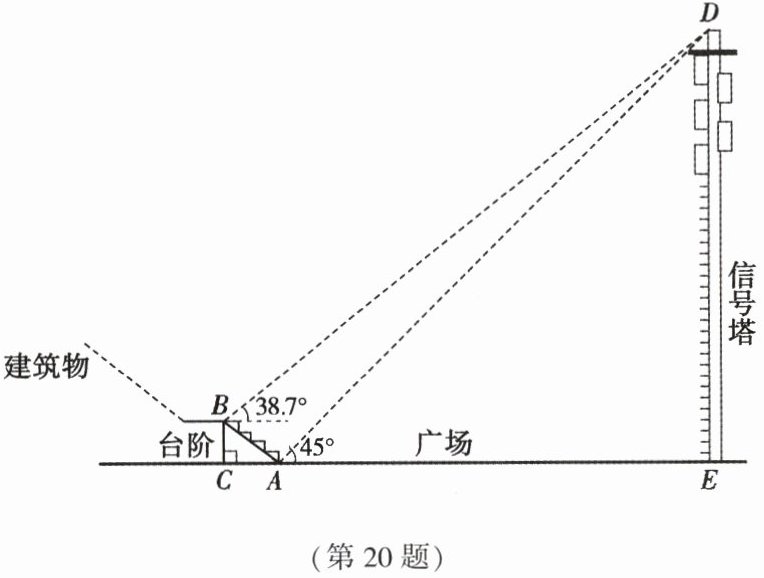
20. (9 分)小王同学学习了锐角三角函数后，通过观察广场的台阶与信号塔之间的相对位置，他认为利用台阶的可测数据与在点 $ A $，$ B $ 处测出点 $ D $ 的仰角度数，可以求出信号塔 $ DE $ 的高。如图，$ AB $ 的长为 $ 5m $，高 $ BC $ 为 $ 3m $。他在点 $ A $ 处测得点 $ D $ 的仰角为 $ 45^{\circ} $，在点 $ B $ 处测得点 $ D $ 的仰角为 $ 38.7^{\circ} $。点 $ A $，$ B $，$ C $，$ D $，$ E $ 在同一平面内。设塔 $ DE $ 的高度为 $ xm $。
(1)用含有 $ x $ 的式子表示线段 $ CE $ 的长：(x + 4)$ m $。
(2)你认为小王同学能求出信号塔 $ DE $ 的高度吗？若能，请求出信号塔 $ DE $ 的高度；若不能，请说明理由。(参考数据：$ \sin 38.7^{\circ} \approx 0.625 $，$ \cos 38.7^{\circ} \approx 0.780 $，$ \tan 38.7^{\circ} \approx 0.80 $。结果保留整数)

答案：
20.
(1)$(x + 4)$
(2)我认为小王同学能求出信号塔$DE$的高度.
如图，过点$B$作$BF \perp DE$，垂足为$F$.

由题意，得$BF = CE = (x + 4)m$，$BC = EF = 3m$. 在$Rt\triangle BDF$中，$\angle DBF = 38.7°$，
$\therefore$ $DF = BF · \tan38.7° \approx 0.8(x + 4)m$. $\because$ $DF + EF = DE$，$\therefore$ $0.8(x + 4) + 3 = x$，
解得$x = 31$，$\therefore$ $DE = 31m$，$\therefore$ 信号塔$DE$的高度约为$31m$.