《2025年基础训练大象出版社九年级数学全一册北师大版》

7. 已知在 $ \triangle ABC $ 中，$ \angle A $，$ \angle B $ 均为锐角，且有 $ |\tan B - \sqrt{3}| + (2\sin A - \sqrt{3})^2 = 0 $，则 $ \triangle ABC $ 是(D)

A.直角(不等腰)三角形
B.等腰直角三角形
C.等腰(不等边)三角形
D.等边三角形

答案： 7.D

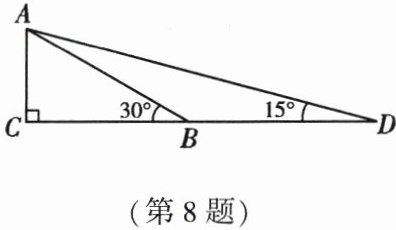
8. 构建几何图形解决代数问题体现了“数形结合”思想的重要性。在计算 $ \tan 15^{\circ} $ 时，如图，在 $ Rt\triangle ACB $ 中，$ \angle C = 90^{\circ} $，$ \angle ABC = 30^{\circ} $，延长 $ CB $ 到点 $ D $，使 $ BD = AB $，连接 $ AD $，得 $ \angle D = 15^{\circ} $，所以 $ \tan 15^{\circ} = \frac{AC}{CD} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3})(2 - \sqrt{3})} = 2 - \sqrt{3} $。类比这种方法，计算 $ \tan 22.5^{\circ} $ 的值为(B)

A.$ \sqrt{2} + 1 $
B.$ \sqrt{2} - 1 $
C.$ \sqrt{2} $
D.$ \frac{1}{2} $

答案： 8.B

9. 已知在 $ \triangle ABC $ 中，$ \angle C = 90^{\circ} $，设 $ \sin B = n $，当 $ \angle B $ 是 $ \triangle ABC $ 中最小的内角时，$ n $ 的取值范围是(A)

A.$ 0 ＜ n \leq \frac{\sqrt{2}}{2} $
B.$ 0 ＜ n \leq \frac{1}{2} $
C.$ 0 ＜ n \leq \frac{\sqrt{3}}{3} $
D.$ 0 ＜ n \leq \frac{\sqrt{3}}{2} $

答案： 9.A

10. 在 $ \triangle ABC $ 中，$ \angle A = 120^{\circ} $，$ AB = 4 $，$ AC = 2 $，则 $ \sin B $ 的值是(D)

A.$ \frac{5\sqrt{7}}{14} $
B.$ \frac{\sqrt{3}}{5} $
C.$ \frac{\sqrt{21}}{7} $
D.$ \frac{\sqrt{21}}{14} $

答案： 10.D

11. 若 $ \angle A $ 是锐角，$ \cos A ＞ \frac{\sqrt{3}}{2} $，则 $ \angle A $ 应满足0° ＜ ∠A ＜ 30°。

答案： 11.$0° ＜ \angle A ＜ 30°$

12. 已知 $ \tan \alpha = 1 $，那么 $ \frac{2\sin \alpha - \cos \alpha}{2\sin \alpha + \cos \alpha} $ 的值等于$\frac{1}{3}$。

答案： 12.$\frac{1}{3}$

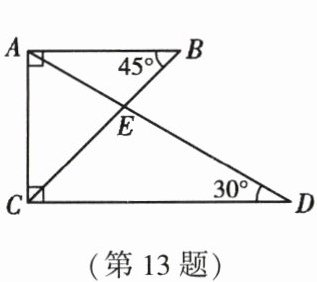
13. 将一副三角尺按如图所示方式叠放在一起，则 $ \frac{BE}{EC} $ 的值是$\frac{\sqrt{3}}{3}$。

答案： 13.$\frac{\sqrt{3}}{3}$

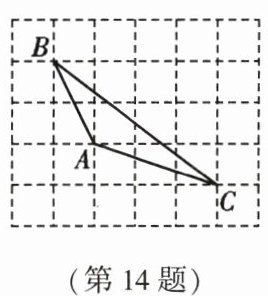
14. 如图，在边长为 1 的小正方形网格中，点 $ A $，$ B $，$ C $ 均在格点上，则 $ \tan B $ 的值为$\frac{1}{2}$。

答案： 14.$\frac{1}{2}$