第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
19. (9 分)(2022·杭州)如图,在 $Rt\triangle ACB$ 中,$\angle ACB = 90^{\circ}$,$M$ 为边 $AB$ 的中点,点 $E$ 在线段 $AM$ 上,$EF \perp AC$ 于点 $F$,连接 $CM$,$CE$。已知 $\angle A = 50^{\circ}$,$\angle ACE = 30^{\circ}$。
(1)求证:$CE = CM$;
(2)若 $AB = 4$,则线段 $FC$ 的长为

(1)求证:$CE = CM$;
(2)若 $AB = 4$,则线段 $FC$ 的长为
$\sqrt{3}$
。
答案:
19.
(1)
∵ ∠ACB = 90°,M为边AB的中点,
∴ MC = MA = MB,
∴ ∠MCA = ∠A,∠MCB = ∠B.
∵ ∠A = 50°,
∴ ∠MCA = 50°,∠MCB = ∠B = 40°,
∴ ∠EMC = ∠MCB + ∠B = 80°,
∵ ∠ACE = 30°,
∴ ∠MEC = ∠A + ∠ACE = 80°,
∴ ∠MEC = ∠EMC,
∴ CE = CM;
(2)$\sqrt{3}$ [提示]
∵ AB = 4,
∴ CE = CM = $\frac{1}{2}$AB = 2.
∵ EF⊥AC,∠ACE = 30°,
∴ EF = $\frac{1}{2}$CE = 1,
∴ FC = $\sqrt{3}$.
(1)
∵ ∠ACB = 90°,M为边AB的中点,
∴ MC = MA = MB,
∴ ∠MCA = ∠A,∠MCB = ∠B.
∵ ∠A = 50°,
∴ ∠MCA = 50°,∠MCB = ∠B = 40°,
∴ ∠EMC = ∠MCB + ∠B = 80°,
∵ ∠ACE = 30°,
∴ ∠MEC = ∠A + ∠ACE = 80°,
∴ ∠MEC = ∠EMC,
∴ CE = CM;
(2)$\sqrt{3}$ [提示]
∵ AB = 4,
∴ CE = CM = $\frac{1}{2}$AB = 2.
∵ EF⊥AC,∠ACE = 30°,
∴ EF = $\frac{1}{2}$CE = 1,
∴ FC = $\sqrt{3}$.
20. (9 分)(2023·内江)如图,在 $\triangle ABC$ 中,$D$ 是 $BC$ 的中点,$E$ 是 $AD$ 的中点,过点 $A$ 作 $AF // BC$ 交 $CE$ 的延长线于点 $F$。
(1)求证:$FA = BD$;
(2)连接 $BF$,若 $AB = AC$,求证:四边形 $ADBF$ 是矩形。
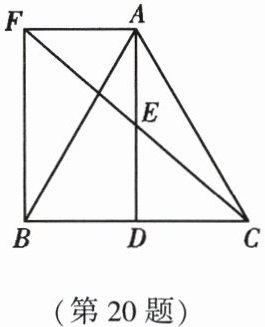
(1)求证:$FA = BD$;
(2)连接 $BF$,若 $AB = AC$,求证:四边形 $ADBF$ 是矩形。

答案:
20.
(1)
∵ AF//BC,
∴ ∠AFE = ∠DCE,∠FAE = ∠CDE.又
∵ E是AD的中点,
∴ AE = DE,
∴ △AEF≌△DEC(AAS),
∴ FA = CD.又
∵ D是BC的中点,
∴ BD = CD,
∴ FA = BD;
(2)
∵ FA = BD,AF//BD,
∴ 四边形ADBF是平行四边形.
∵ AB = AC,D是BC的中点,
∴ AD⊥BC,
∴ ∠ADB = 90°,
∴ 平行四边形ADBF是矩形,
∴ 四边形ADBF是矩形.
(1)
∵ AF//BC,
∴ ∠AFE = ∠DCE,∠FAE = ∠CDE.又
∵ E是AD的中点,
∴ AE = DE,
∴ △AEF≌△DEC(AAS),
∴ FA = CD.又
∵ D是BC的中点,
∴ BD = CD,
∴ FA = BD;
(2)
∵ FA = BD,AF//BD,
∴ 四边形ADBF是平行四边形.
∵ AB = AC,D是BC的中点,
∴ AD⊥BC,
∴ ∠ADB = 90°,
∴ 平行四边形ADBF是矩形,
∴ 四边形ADBF是矩形.
21. (10 分)如图,在矩形 $ABCD$ 中,$P$ 是线段 $AD$ 上一动点,$O$ 为 $BD$ 的中点,$PO$ 的延长线交 $BC$ 于点 $Q$。
(1)求证:$OP = OQ$。
(2)若 $AD = 8cm$,$AB = 6cm$,点 $P$ 从点 $A$ 出发,以 $1cm/s$ 的速度向点 $D$ 运动(不与点 $D$ 重合)。设点 $P$ 运动时间为 $ts$,请用含 $t$ 的式子表示 $PD$ 的长,并求 $t$ 为何值时,四边形 $PBQD$ 是菱形。
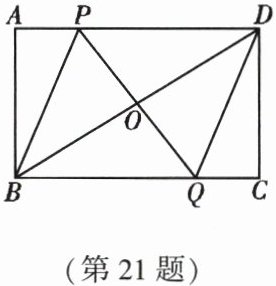
(1)求证:$OP = OQ$。
(2)若 $AD = 8cm$,$AB = 6cm$,点 $P$ 从点 $A$ 出发,以 $1cm/s$ 的速度向点 $D$ 运动(不与点 $D$ 重合)。设点 $P$ 运动时间为 $ts$,请用含 $t$ 的式子表示 $PD$ 的长,并求 $t$ 为何值时,四边形 $PBQD$ 是菱形。

答案:
21.
(1)
∵ 四边形ABCD是矩形,
∴ AD//BC,
∴ ∠PDO = ∠QBO.又
∵ OB = OD,∠POD = ∠QOB,
∴ △POD≌△QOB,
∴ OP = OQ;
(2)由题意,得PD = 8 - t,
∵ OP = OQ,OB = OD,
∴ 四边形PBQD是平行四边形.当PB = PD时,▱PBQD是菱形,
∴ PB = PD = 8 - t.在Rt△ABP中,AP² + AB² = BP²,
∴ t² + 6² = (8 - t)²,
∴ t = $\frac{7}{4}$.
∴ 当t = $\frac{7}{4}$s时,四边形PBQD是菱形.
(1)
∵ 四边形ABCD是矩形,
∴ AD//BC,
∴ ∠PDO = ∠QBO.又
∵ OB = OD,∠POD = ∠QOB,
∴ △POD≌△QOB,
∴ OP = OQ;
(2)由题意,得PD = 8 - t,
∵ OP = OQ,OB = OD,
∴ 四边形PBQD是平行四边形.当PB = PD时,▱PBQD是菱形,
∴ PB = PD = 8 - t.在Rt△ABP中,AP² + AB² = BP²,
∴ t² + 6² = (8 - t)²,
∴ t = $\frac{7}{4}$.
∴ 当t = $\frac{7}{4}$s时,四边形PBQD是菱形.
查看更多完整答案,请扫码查看


