第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 已知在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \sin A = \frac{3}{5} $,则 $ \tan B $ 的值为(
A.$ \frac{4}{3} $
B.$ \frac{4}{5} $
C.$ \frac{5}{4} $
D.$ \frac{3}{4} $
A
)A.$ \frac{4}{3} $
B.$ \frac{4}{5} $
C.$ \frac{5}{4} $
D.$ \frac{3}{4} $
答案:
1.A
2. 如图,$ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,点 $ D $ 在 $ AC $ 上,$ \angle DBC = \angle A $。若 $ AC = 4 $,$ \cos A = \frac{4}{5} $,则线段 $ BD $ 的长度为(
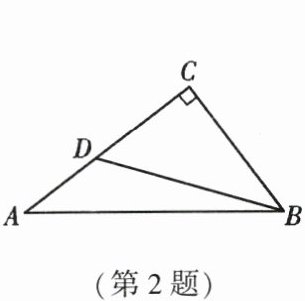
A.$ \frac{9}{4} $
B.$ \frac{12}{5} $
C.$ \frac{15}{4} $
D.$ 4 $
C
)
A.$ \frac{9}{4} $
B.$ \frac{12}{5} $
C.$ \frac{15}{4} $
D.$ 4 $
答案:
2.C
3. 数学家笛卡儿在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短。在菱形 $ ABCD $ 中,$ AB = 2 $,$ \angle DAB = 120^{\circ} $。如图,建立平面直角坐标系 $ xOy $,使得边 $ AB $ 在 $ x $ 轴正半轴上,点 $ D $ 在 $ y $ 轴正半轴上,则 $ C $ 的坐标是(

A.$ (1,\sqrt{3}) $
B.$ (\sqrt{3},1) $
C.$ (2,\sqrt{3}) $
D.$ (\sqrt{2},2) $
C
)
A.$ (1,\sqrt{3}) $
B.$ (\sqrt{3},1) $
C.$ (2,\sqrt{3}) $
D.$ (\sqrt{2},2) $
答案:
3.C
4. 如图,河堤横断面迎水坡 $ AB $ 的坡度是 $ 1 : \sqrt{3} $,堤高 $ BC = 8m $,则坡面 $ AB $ 的长度是(
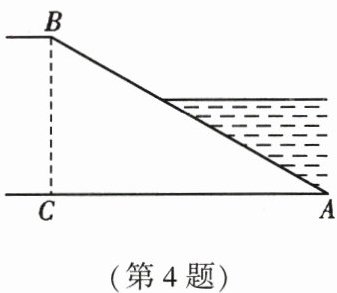
A.$ 16m $
B.$ 16\sqrt{3}m $
C.$ 8m $
D.$ 8\sqrt{3}m $
A
)
A.$ 16m $
B.$ 16\sqrt{3}m $
C.$ 8m $
D.$ 8\sqrt{3}m $
答案:
4.A
5. 在 $ \triangle ABC $ 中,$ AB = 12\sqrt{2} $,$ AC = 13 $,$ \cos B = \frac{\sqrt{2}}{2} $,则 $ BC $ 边的长为(
A.$ 7 $
B.$ 8 $
C.$ 8 $ 或 $ 17 $
D.$ 7 $ 或 $ 17 $
D
)A.$ 7 $
B.$ 8 $
C.$ 8 $ 或 $ 17 $
D.$ 7 $ 或 $ 17 $
答案:
5.D
6. 如图,在 $ \triangle ABC $ 中,$ AC = 5 $,$ \cos B = \frac{\sqrt{2}}{2} $,$ \sin C = \frac{3}{5} $,则 $ \triangle ABC $ 的面积是(
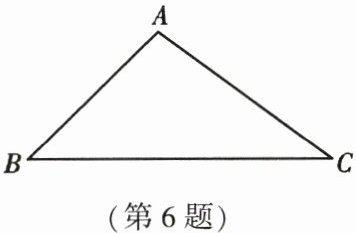
A.$ 14 $
B.$ 12 $
C.$ \frac{21}{2} $
D.$ 21 $
C
)
A.$ 14 $
B.$ 12 $
C.$ \frac{21}{2} $
D.$ 21 $
答案:
6.C
查看更多完整答案,请扫码查看


