《2025年基础训练大象出版社九年级数学全一册北师大版》

20. （9 分）某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系. 每盆植入 $3$ 株时，平均单株盈利 $3$ 元；以同样的栽培条件，若每盆每增加 $1$ 株，平均单株盈利就减少 $0.5$ 元. 要使每盆的盈利达到 $10$ 元，每盆应该植多少株？

答案： 设每盆花苗增加$x$株,则每盆花苗有$(x+3)$株,平均单株盈利为$(3-0.5x)$元,由题意,得$(x+3)(3-0.5x)=10$. ……5分
化简整理,得$x^2-3x+2=0$.解这个方程,得$x_1=1$,$x_2=2$.
则$3+1=4$,$2+3=5$.
$\therefore$要使每盆的盈利达到10元,每盆应该植入4株或5株. ……9分

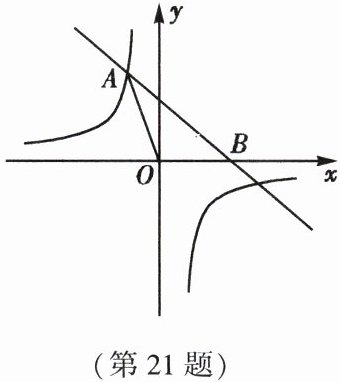
21. （10 分）如图，已知直线 $y = -x + 4$ 与反比例函数 $y = \frac{k}{x}$ 的图象相交于点 $A(-2, a)$，并且与 $x$ 轴相交于点 $B$.
(1) 求 $a$ 的值；
(2) 求反比例函数的表达式；
(3) 求 $\triangle AOB$ 的面积.

答案：

(1)将$A(-2,a)$代入$y=-x+4$中,得$a=-(-2)+4$,所以$a=6$. ……3分
(2)由
(1)得$A(-2,6)$,将$A(-2,6)$代入$y=\frac{k}{x}$中,得$6=\frac{k}{-2}$,即$k=-12$. ……4分
所以反比例函数的表达式为$y=-\frac{12}{x}$. ……5分
(3)如下图,过$A$点作$AD\perp x$轴于点$D$,
因为$A$点坐标为$(-2,6)$,所以$AD=6$. ……7分
在直线$y=-x+4$中,令$y=0$,得$x=4$,所以$B$点坐标为$(4,0)$,即$OB=4$.
所以$\triangle AOB$的面积$S=\frac{1}{2}× OB× AD=\frac{1}{2}×4×6=12$.
……10分

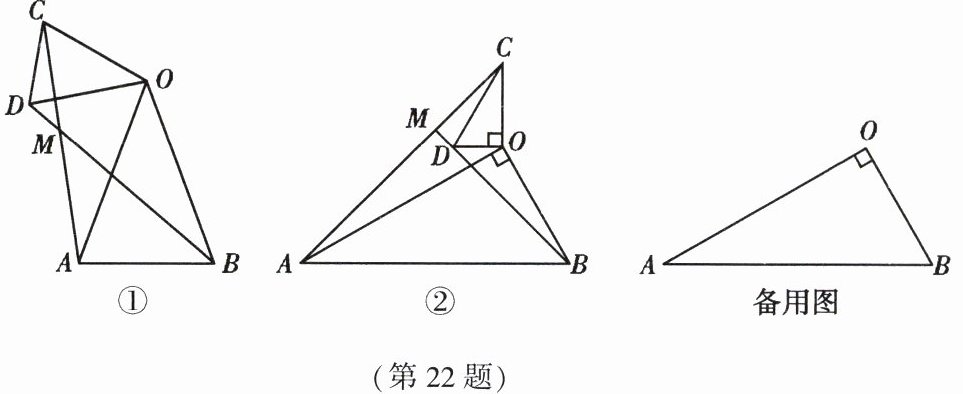
22. (10 分)(1) 问题发现：如图①，在 $\triangle OAB$ 和 $\triangle OCD$ 中，$OA = OB$，$OC = OD$，$\angle AOB = \angle COD = 40°$，连接 $AC$，$BD$ 交于点 $M$. 填空：
①$\frac{AC}{BD}$ 的值为1；②$\angle AMB$ 的度数为40°.
(2) 类比探究：如图②，在 $\triangle OAB$ 和 $\triangle OCD$ 中，$\angle AOB = \angle COD = 90°$，$\angle OAB = \angle OCD = 30°$，连接 $AC$ 交 $BD$ 的延长线于点 $M$. 请判断 $\frac{AC}{BD}$ 的值及 $\angle AMB$ 的度数，并说明理由.
(3) 拓展延伸：在 (2) 的条件下，将 $\triangle OCD$ 绕点 $O$ 在平面内旋转，$AC$，$BD$ 所在直线交于点 $M$. 若 $OD = 1$，$OB = \sqrt{7}$，请直接写出当点 $C$ 与点 $M$ 重合时 $AC$ 的长.

答案：

(1)①$1$ ……1分
②$40°$(注:若填为40,不扣分) ……2分
(2)$\frac{AC}{BD}=\sqrt{3}$,$\angle AMB=90°$.(注:若无判断,但后续证明正确,不扣分) ……4分
理由如下:$\because \angle AOB=\angle COD=90°$,$\angle OAB=\angle OCD=30°$,
$\therefore \frac{CO}{DO}=\frac{AO}{BO}=\sqrt{3}$.
又$\because \angle COD+\angle AOD=\angle AOB+\angle AOD$,$\therefore \angle AOC=\angle BOD$.
$\therefore \triangle AOC\sim\triangle BOD$. ……6分
$\therefore \frac{AC}{BD}=\frac{CO}{DO}=\sqrt{3}$,$\angle CAO=\angle DBO$.
$\because \angle AOB=90°$,$\therefore \angle DBO+\angle ABD+\angle BAO=90°$.
$\therefore \angle CAO+\angle ABD+\angle BAO=90°$.$\therefore \angle AMB=90°$.
……8分
(3)$AC$的长为$2\sqrt{3}$或$3\sqrt{3}$. ……10分
【提示】在$\triangle OCD$旋转过程中,
(2)中的结论仍成立,即$\frac{AC}{BD}=\sqrt{3}$,$\angle AMB=90°$.如图所示,当点$C$与点$M$重合时,$AC_1$,$AC_2$的长即为所求.