《2025年基础训练大象出版社九年级数学全一册北师大版》

18. （9 分）杨华与季红用 $5$ 张规格相同的硬纸片做拼图游戏，正面如图①所示，背面完全一样，将它们背面朝上搅匀后，同时抽出两张. 规则如下：
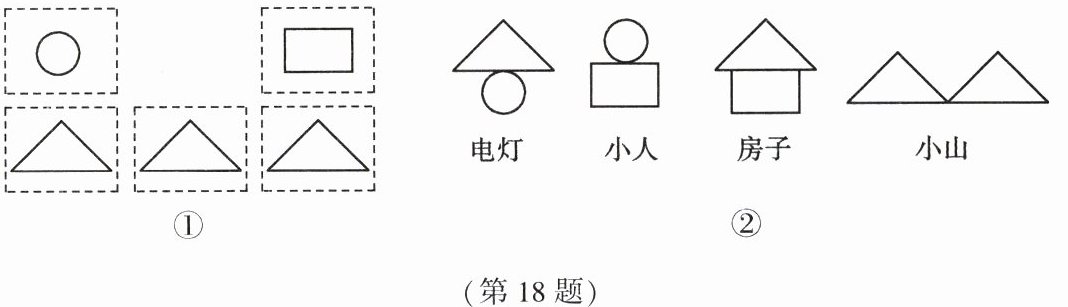
当两张硬纸片上的图形可拼成电灯或小人时，杨华得 $1$ 分；当两张硬纸片上的图形可拼成房子或小山时，季红得 $1$ 分（如图②）.
游戏规则对双方公平吗？请说明理由. 若你认为不公平，如何修改游戏规则才能使游戏对双方公平？

答案： 不公平. ……1分
因为杨华胜的概率为$0.4$,季红胜的概率为$0.6$.
……5分
应改为当两张硬纸片上的图形可拼成电灯或小人时,杨华得3分;当两张硬纸片上的图形可拼成房子或小山时,季红得2分. ……9分

19. （9 分）如图，在 $\triangle ABC$ 中，点 $D$，$E$，$F$ 分别在 $AB$，$BC$，$AC$ 边上，$DE // AC$，$EF // AB$.
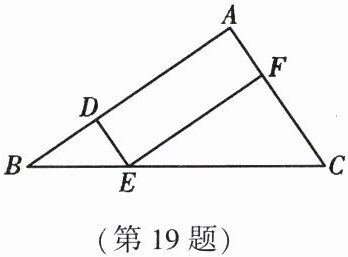
(1) 求证：$\triangle BDE \backsim \triangle EFC$.
(2) 设 $\frac{AF}{FC} = \frac{1}{2}$.
①若 $BC = 12$，求线段 $BE$ 的长；
②若 $\triangle EFC$ 的面积是 $20$，求 $\triangle ABC$ 的面积.

答案：
(1)$\because DE// AC$,
$\therefore \angle DEB=\angle FCE$. ……1分
$\because EF// AB$,
$\therefore \angle DBE=\angle FEC$, ……2分
$\therefore \triangle BDE\sim\triangle EFC$. ……3分
(2)①$\because EF// AB$,
$\therefore \frac{BE}{EC}=\frac{AF}{FC}=\frac{1}{2}$. ……4分
$\because EC=BC-BE=12-BE$,
$\therefore \frac{BE}{12-BE}=\frac{1}{2}$, ……5分
解得$BE=4$(符合题意). ……6分
②$\because \frac{AF}{FC}=\frac{1}{2}$,
$\therefore \frac{FC}{AC}=\frac{2}{3}$. ……7分
$\because EF// AB$,
$\therefore \angle CFE=\angle CAB$,$\angle CEF=\angle CBA$,
$\therefore \triangle EFC\sim\triangle BAC$, ……8分
$\therefore \frac{S_{\triangle EFC}}{S_{\triangle ABC}}=(\frac{FC}{AC})^2=(\frac{2}{3})^2=\frac{4}{9}$,
$\therefore S_{\triangle ABC}=\frac{9}{4}S_{\triangle EFC}=\frac{9}{4}×20=45$. ……9分