第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
22. (8 分)(2023·达州)【背景】在一次物理实验中,小冉同学用一固定电压为 12V 的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡 L(灯丝的阻值 $ R_L = 2\Omega $)亮度的实验(如图)。已知串联电路中,电流与电阻 $ R $、$ R_L $ 之间关系为 $ I = \frac{U}{R + R_L} $,通过实验得出如下数据:
(1)$ a = $
(2)【探究】根据以上实验,构建出函数 $ y = \frac{12}{x + 2}(x \geq 0) $,结合表格信息,探究函数 $ y = \frac{12}{x + 2}(x \geq 0) $ 的图象与性质。

① 在平面直角坐标系中画出对应函数 $ y = \frac{12}{x + 2}(x \geq 0) $ 的图象;
② 随着自变量 $ x $ 的不断增大,函数值 $ y $ 的变化趋势是
(3)【拓展】结合(2)中函数图象分析,当 $ x \geq 0 $ 时,$ \frac{12}{x + 2} \geq -\frac{3}{2}x + 6 $ 的解集为
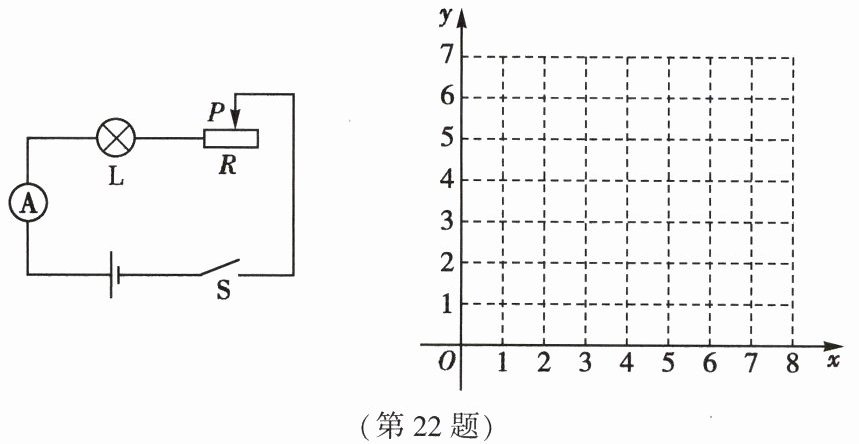
(1)$ a = $
2
,$ b = $1.5
。(2)【探究】根据以上实验,构建出函数 $ y = \frac{12}{x + 2}(x \geq 0) $,结合表格信息,探究函数 $ y = \frac{12}{x + 2}(x \geq 0) $ 的图象与性质。

① 在平面直角坐标系中画出对应函数 $ y = \frac{12}{x + 2}(x \geq 0) $ 的图象;
② 随着自变量 $ x $ 的不断增大,函数值 $ y $ 的变化趋势是
不断减小
。(3)【拓展】结合(2)中函数图象分析,当 $ x \geq 0 $ 时,$ \frac{12}{x + 2} \geq -\frac{3}{2}x + 6 $ 的解集为
$x \geq 2$或$x = 0$
。
答案:
22.
(1)2 1.5
(2)①图略 ②不断减小
(3)$x \geq 2$或$x = 0$
(1)2 1.5
(2)①图略 ②不断减小
(3)$x \geq 2$或$x = 0$
23. (12 分)如图,在平面直角坐标系中,一次函数 $ y_1 = kx + b $ 的图象分别交 $ x $ 轴、$ y $ 轴于 $ A $,$ B $ 两点,与反比例函数 $ y_2 = \frac{n}{x} $ 的图象交于 $ C $,$ D $ 两点。已知点 $ C $ 的坐标为 $ (-4,-1) $,点 $ D $ 的横坐标为 2。
(1)求反比例函数与一次函数的解析式。
(2)直接写出当 $ x $ 为何值时 $ y_1 > y_2 $。
(3)点 $ P $ 是反比例函数在第一象限的图象上的点,且点 $ P $ 的横坐标大于 2,过点 $ P $ 作 $ x $ 轴的垂线,垂足为 $ E $。当 $ \triangle APE $ 的面积为 3 时,求点 $ P $ 的坐标。
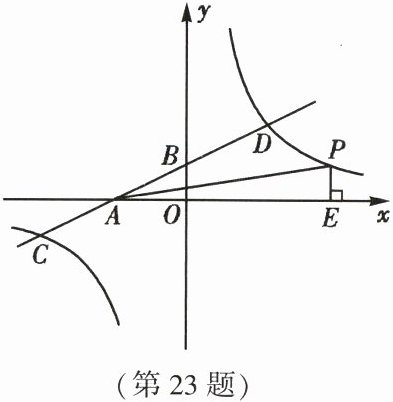
(1)求反比例函数与一次函数的解析式。
(2)直接写出当 $ x $ 为何值时 $ y_1 > y_2 $。
(3)点 $ P $ 是反比例函数在第一象限的图象上的点,且点 $ P $ 的横坐标大于 2,过点 $ P $ 作 $ x $ 轴的垂线,垂足为 $ E $。当 $ \triangle APE $ 的面积为 3 时,求点 $ P $ 的坐标。

答案:
23.
(1)
∵点$C( - 4, - 1)$在反比例函数$y_2 = \frac {n}{x}$的图象上,
∴$- 1 = - \frac {n}{4}$,
∴$n = 4$,
∴反比例函数的解析式为$y_2 = \frac {4}{x}$.
∵点$D$的横坐标为2,
∴点$D$的坐标为$(2,2)$.
把点$C$,$D$的坐标代入一次函数$y_1 = kx + b$,可得$\begin{cases} - 4k + b = - 1 \\ 2k + b = 2 \end{cases}$,
解得$\begin{cases} k = \frac {1}{2} \\ b = 1 \end{cases}$,
∴一次函数的解析式为$y_1 = \frac {1}{2}x + 1$.
(2)$- 4 < x < 0$或$x > 2$.
(3)当$y_1 = 0$时,$\frac {1}{2}x + 1 = 0$,解得$x = - 2$.
∴点$A$的坐标为$( - 2,0)$.
设点$P$的坐标为$(m,\frac {4}{m})$.
∵$\triangle APE$的面积为3,
∴$\frac {1}{2}(m + 2) · \frac {4}{m} = 3$,解得$m = 4$.
经检验,$m = 4$符合题意.
∴点$P$的坐标为$(4,1)$.
(1)
∵点$C( - 4, - 1)$在反比例函数$y_2 = \frac {n}{x}$的图象上,
∴$- 1 = - \frac {n}{4}$,
∴$n = 4$,
∴反比例函数的解析式为$y_2 = \frac {4}{x}$.
∵点$D$的横坐标为2,
∴点$D$的坐标为$(2,2)$.
把点$C$,$D$的坐标代入一次函数$y_1 = kx + b$,可得$\begin{cases} - 4k + b = - 1 \\ 2k + b = 2 \end{cases}$,
解得$\begin{cases} k = \frac {1}{2} \\ b = 1 \end{cases}$,
∴一次函数的解析式为$y_1 = \frac {1}{2}x + 1$.
(2)$- 4 < x < 0$或$x > 2$.
(3)当$y_1 = 0$时,$\frac {1}{2}x + 1 = 0$,解得$x = - 2$.
∴点$A$的坐标为$( - 2,0)$.
设点$P$的坐标为$(m,\frac {4}{m})$.
∵$\triangle APE$的面积为3,
∴$\frac {1}{2}(m + 2) · \frac {4}{m} = 3$,解得$m = 4$.
经检验,$m = 4$符合题意.
∴点$P$的坐标为$(4,1)$.
查看更多完整答案,请扫码查看


