《2025年基础训练大象出版社九年级数学全一册北师大版》

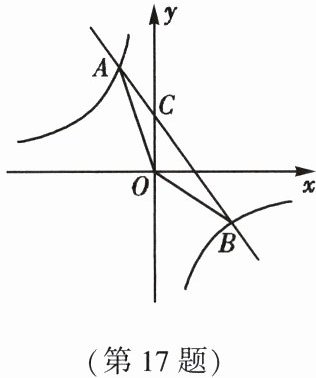
17. （8 分）（2023·东营）如图，在平面直角坐标系中，一次函数 $ y = ax + b(a ＜ 0) $ 与反比例函数 $ y = \frac{k}{x}(k \neq 0) $ 交于 $ A(-m,3m) $，$ B(4,-3) $ 两点，与 $ y $ 轴交于点 $ C $，连接 $ OA $，$ OB $。
（1）求反比例函数和一次函数的表达式；
（2）求 $ \triangle AOB $ 的面积。

答案： 17.
(1)
∵点$B(4, - 3)$在反比例函数$y = \frac {k}{x}$的图象上，
∴$- 3 = \frac {k}{4}$，
∴$k = - 12$，
∴反比例函数的表达式为$y = - \frac {12}{x}$.
∵$A( - m,3m)$在反比例函数$y = - \frac {12}{x}$的图象上，
∴$3m = - \frac {12}{ - m}$，
∴$m_1 = 2$，$m_2 = - 2$(舍去)，
∴点$A$的坐标为$( - 2,6)$.
∵点$A$，$B$在一次函数$y = ax + b$的图象上，把点$A( - 2,6)$，$B(4, - 3)$分别代入，得$\begin{cases} - 2a + b = 6 \\ 4a + b = - 3 \end{cases}$，
解得$\begin{cases} a = - \frac {3}{2} \\ b = 3 \end{cases}$，
∴一次函数的表达式为$y = - \frac {3}{2}x + 3$.
综上可知，反比例函数的表达式为$y = - \frac {12}{x}$，一次函数的表达式为$y = - \frac {3}{2}x + 3$.
(2)
∵$C$为直线$AB$与$y$轴的交点，
∴$OC = 3$，
∴$S_{\triangle AOB} = S_{\triangle AOC} + S_{\triangle BOC} = \frac {1}{2} · OC · |x_A| + \frac {1}{2} · OC · |x_B| = \frac {1}{2}×3×2 + \frac {1}{2}×3×4 = 9$.

18. （9 分）（2023·贵州）如图，在平面直角坐标系中，四边形 $ OABC $ 是矩形，反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象分别与 $ AB $，$ BC $ 交于点 $ D(4,1) $ 和点 $ E $，且 $ D $ 为 $ AB $ 的中点。
（1）求反比例函数的表达式和点 $ E $ 的坐标；
（2）若一次函数 $ y = x + m $ 与反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象相交于点 $ M $，当点 $ M $ 在反比例函数图象上点 $ D $，$ E $ 之间的部分时（点 $ M $ 可与点 $ D $，$ E $ 重合），直接写出 $ m $ 的取值范围。

答案： 18.
(1)
∵四边形$OABC$是矩形，点$D(4,1)$，且$D$为$AB$的中点，
∴点$B$的坐标为$(4,2)$，
∴点$E$的纵坐标为2.
∵反比例函数$y = \frac {k}{x}(x ＞ 0)$的图象分别与$AB$，$BC$交于点$D(4,1)$和点$E$，
∴$k = 4×1 = 4$，
∴反比例函数的表达式为$y = \frac {4}{x}$.
把$y = 2$代入，得$2 = \frac {4}{x}$，
解得$x = 2$，
∴点$E$的坐标为$(2,2)$.
综上可知，反比例函数的表达式为$y = \frac {4}{x}$，点$E$的坐标为$(2,2)$.
(2)$- 3 \leq m \leq 0$.【提示】把$D(4,1)$代入$y = x + m$，得$1 = 4 + m$，解得$m = - 3$.
把$E(2,2)$代入$y = x + m$，得$2 = 2 + m$，解得$m = 0$.
∴$m$的取值范围是$- 3 \leq m \leq 0$.

19. （10 分）（2022·河南）如图，反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象经过点 $ A(2,4) $ 和点 $ B $，点 $ B $ 在点 $ A $ 的下方，$ AC $ 平分 $ \angle OAB $，交 $ x $ 轴于点 $ C $。
（1）求反比例函数的表达式。
（2）请用无刻度的直尺和圆规作出线段 $ AC $ 的垂直平分线。（要求：不写作法，保留作图痕迹，使用 2B 铅笔作图）
（3）线段 $ OA $ 与（2）中所作的垂直平分线相交于点 $ D $，连接 $ CD $。求证：$ CD // AB $。

答案：
19.
(1)
∵反比例函数$y = \frac {k}{x}$的图象经过点$A(2,4)$，
∴$k = 2×4 = 8$.
∴反比例函数的表达式为$y = \frac {8}{x}$.
(2)如图:

(3)
∵$AC$平分$\angle OAB$，
∴$\angle OAC = \angle BAC$.
∵$AC$的垂直平分线交$OA$于点$D$，
∴$DA = DC$，
∴$\angle DAC = \angle DCA$，
∴$\angle DCA = \angle BAC$，
∴$CD// AB$.