《2025年基础训练大象出版社九年级数学全一册北师大版》

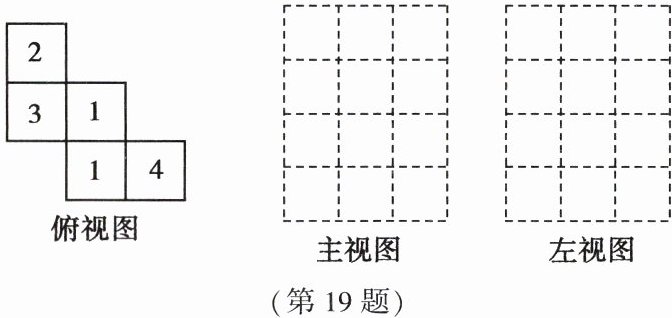
19. （10 分）如图是一个几何体的俯视图，正方形中的数字是该位置上的小立方体的数量.
（1）请画出这个几何体的主视图和左视图；
（2）若其中每个小立方体的棱长为 $ 1cm $，求这个几何体的表面积（含底面）.

答案：
19.
(1)主视图、左视图如图所示:
投影与视图
　　　　 　　
(2)这个几何体的表面积为$8 + 8 + 5 + 5 + 9 + 9 = 44(cm^2)$。

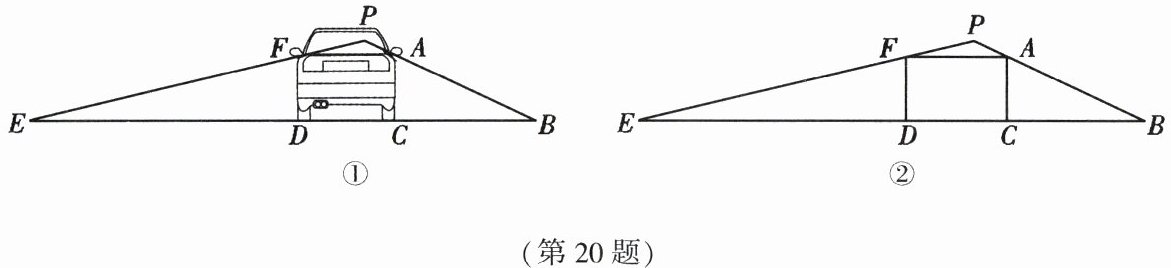
20. （9 分）汽车盲区是指驾驶员位于正常驾驶座位置时（如图①），其视线被车体遮挡而不能直接观察到的那部分区域. 预防进入汽车盲区，能有效防止交通事故发生，提高学生避险能力. 小明在学习了交通安全知识后，对汽车盲区产生了兴趣. 图②是他研究的一个汽车盲区的示意图，$ EB $ 为驾驶员的盲区，驾驶员的眼睛点 $ P $ 处与地面 $ EB $ 的距离为 $ 1.5m $，车宽 $ AF = 1.8m $，车头 $ FACD $ 近似看成一个矩形，且满足 $ 3DF = 2AF $，求汽车盲区 $ EB $ 的长度.

答案：
20.如图，过点P作PN⊥EB于点N，交AF于点M。

∵$3DF = 2AF$，$AF = 1.8m$，
∴$DF = 1.2m$。
∵四边形FACD是矩形，
∴∠FDC = 90°，AF//CD，
∴DF⊥DC。
∵MN⊥DC，
∴DF = MN = 1.2m。
∵PN = 1.5m，
∴PM = PN - MN = 1.5 - 1.2 = 0.3(m)。
∵AF//EB，
∴∠PFA = ∠PEB，∠PAF = ∠PBE，
∴△PAF∽△PBE，
∴$\frac{AF}{EB} = \frac{PM}{PN}$，$\frac{1.8}{EB} = \frac{0.3}{1.5}$，
∴$EB = 9m$，
∴汽车盲区EB的长度为9m。

21. （10 分）如图，在一个阳光明媚的上午，陈老师组织学生测量小山坡上的一棵大树 $ CD $ 的高度，山坡 $ OM $ 与地面 $ ON $ 的夹角为 $ 30^{\circ} $（$ \angle MON = 30^{\circ} $），站立在水平地面上身高 1.7 米的小明 $ AB $ 在地面上的影长 $ BP $ 为 1.2 米，此刻大树 $ CD $ 在斜坡上的影长 $ DQ $ 为 5 米，求大树 $ CD $ 的高度.

答案：
21.如图，过点Q作QE⊥DC于点E，由题意，可得$\frac{AB}{BP} = \frac{CE}{EQ}$。

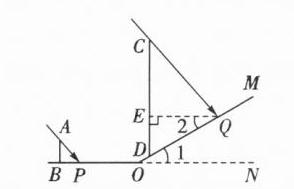
∵EQ//NO，
∴∠1 = ∠2 = 30°。又
∵QD = 5，
∴$DE = \frac{5}{2}$，$EQ = \frac{5\sqrt{3}}{2}$，
∴$\frac{1.7}{1.2} = \frac{CE}{\frac{5\sqrt{3}}{2}}$，解得$CE = \frac{85\sqrt{3}}{24}$。
∴$CD = CE + DE = \frac{60 + 85\sqrt{3}}{24}$，
∴大树CD的高度为$\frac{60 + 85\sqrt{3}}{24}$米。