第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
15. 棱长是 $ 1cm $ 的小立方体组成如图所示的几何体,那么这个几何体的表面积是
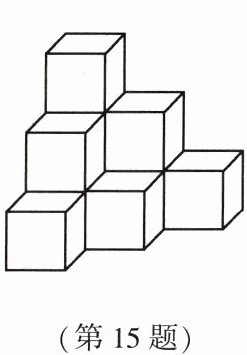
36
$ cm^{2} $.
答案:
15.36
16. (9 分)试确定图中路灯的位置,并画出此时小明在路灯下的影子.
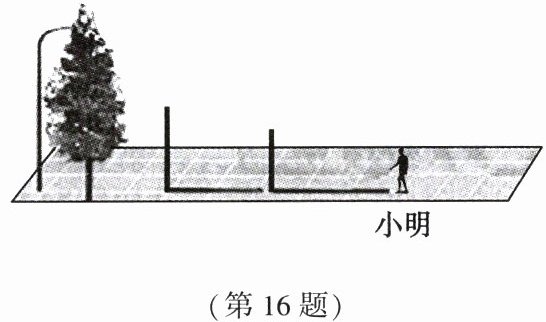

答案:
16.如图:

16.如图:

17. (9 分)如图,在平面直角坐标系中,点 $ P(2,3) $ 是一个光源,木杆 $ AB $ 两端的坐标分别为 $ A(0,1) $,$ B(3,1) $,求木杆 $ AB $ 在 $ x $ 轴上的投影 $ CD $ 的长度.
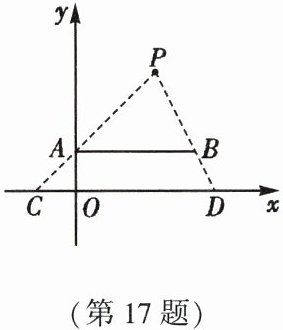

答案:
17.如图,过点P作PM⊥x轴,垂足为M,交AB于点N.
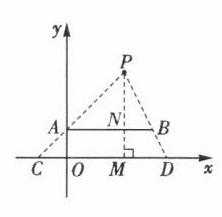
∵点P(2,3),A(0,1),B(3,1),
∴OM=AN=2,AB=3,PN=2,PM=3.
∵AB//CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴$\frac{PN}{PM} = \frac{AB}{CD}$,即$\frac{2}{3} = \frac{3}{CD}$,
∴$CD=\frac{9}{2}$,
故木杆AB在x轴上的投影CD的长度为$\frac{9}{2}$。
17.如图,过点P作PM⊥x轴,垂足为M,交AB于点N.

∵点P(2,3),A(0,1),B(3,1),
∴OM=AN=2,AB=3,PN=2,PM=3.
∵AB//CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴$\frac{PN}{PM} = \frac{AB}{CD}$,即$\frac{2}{3} = \frac{3}{CD}$,
∴$CD=\frac{9}{2}$,
故木杆AB在x轴上的投影CD的长度为$\frac{9}{2}$。
18. (8 分)图中的几何体是用 10 个相同的小正方体搭成的,其左视图如图所示.
(1)请在方格纸中用实线画出该几何体的主视图、俯视图.
(2)如果保持这个几何体的俯视图和左视图不变,那么最多可以添加几个小正方体?最多可以拿掉几个小正方体?
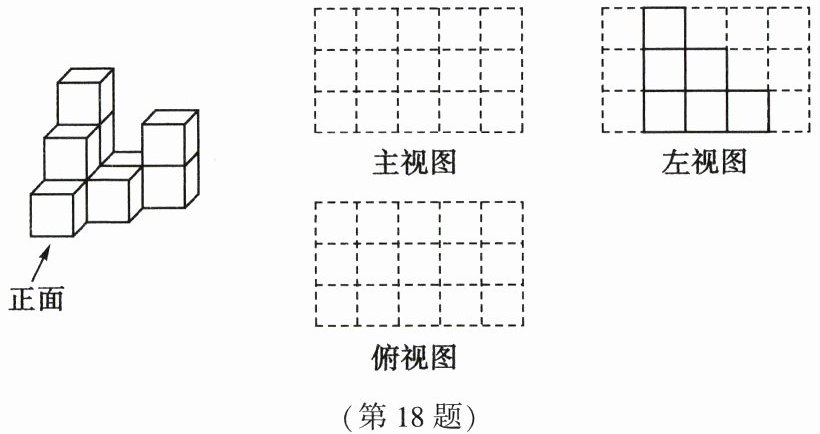
(1)请在方格纸中用实线画出该几何体的主视图、俯视图.
(2)如果保持这个几何体的俯视图和左视图不变,那么最多可以添加几个小正方体?最多可以拿掉几个小正方体?

答案:
18.
(1)如图.


(2)如果保持这个几何体的俯视图和左视图不变,那么最多可以添加4个小正方体,最多可以拿掉1个小正方体。
18.
(1)如图.


(2)如果保持这个几何体的俯视图和左视图不变,那么最多可以添加4个小正方体,最多可以拿掉1个小正方体。
查看更多完整答案,请扫码查看


