《2025年基础训练大象出版社九年级数学全一册北师大版》

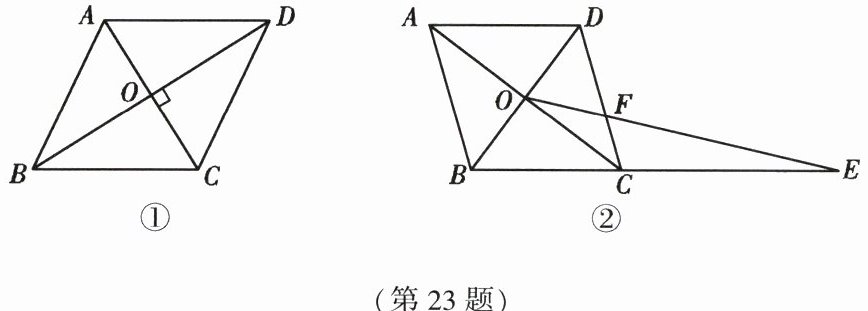
23. （12分）（2023·江西）【课本再现】

【定理证明】
（1）为了证明该定理，小明同学画出了图形（如图①），并写出了“已知”和“求证”，请你完成证明过程。
已知：在$□ ABCD$中，对角线$BD \perp AC$，垂足为$O$。
求证：$□ ABCD$是菱形。
【知识应用】
（2）如图②，在$□ ABCD$中，对角线$AC$和$BD$相交于点$O$，$AD = 5$，$AC = 8$，$BD = 6$。
①求证：$□ ABCD$是菱形；
②延长$BC$至点$E$，连接$OE$交$CD$于点$F$，若$\angle E = \frac{1}{2}\angle ACD$，求$\frac{OF}{EF}$的值。

答案：
23.
(1)
∵　四边形ABCD是平行四边形，AC与BD 交于点O，
∴　BO=DO.
又
∵　BD⊥AC，垂足为O，
∴　AC是BD的垂直平分线，
∴　AB=AD，
∴　▱ABCD是菱形.
(2)①
∵　在▱ABCD中，对角线AC和BD相交于点O，AC=8，BD=6，
∴　AO=CO=$\frac{1}{2}$AC=4，DO=$\frac{1}{2}$BD=3.
又
∵　AD=5，
∴　在△AOD中，AD²=AO²+DO²，
∴　∠AOD=90°，
即BD⊥AC，
∴　▱ABCD是菱形.
　　　　　　　 ②如图，设CD的中点为G，连接OG，
∴　OG是△ACD的中位线，
∴　OG=$\frac{1}{2}$AD=$\frac{5}{2}$.
由①知，四边形ABCD是菱形，
∴　∠ACD=∠ACB.
又
∵　∠E=$\frac{1}{2}$∠ACD，
∴　∠E=$\frac{1}{2}$∠ACB.
又
∵　∠ACB=∠E+∠COE，
∴　∠E=∠COE，
∴　CE=CO=4.
∵　OG是△ACD的中位线，
∴　OG//AD//BE，
∴　△OGF∽△ECF，
∴　$\frac{OF}{EF}$=$\frac{OG}{CE}$.
又
∵　OG=$\frac{5}{2}$，CE=4，
∴　$\frac{OF}{EF}$=$\frac{\frac{5}{2}}{4}$=$\frac{5}{8}$