第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
6. (2024·河南)如图,在$□ ABCD$中,对角线$AC$,$BD$相交于点$O$,点$E$为$OC$的中点,$EF // AB$交$BC$于点$F$。若$AB = 4$,则$EF$的长为 (

A.$\frac{1}{2}$
B.1
C.$\frac{4}{3}$
D.2
B
)
A.$\frac{1}{2}$
B.1
C.$\frac{4}{3}$
D.2
答案:
6.B
7. 如图,点$O$是等边三角形$PQR$的中心,$P'$,$Q'$,$R'$分别是$OP$,$OQ$,$OR$的中点。此时,$\triangle P'Q'R'$与$\triangle PQR$的位似比、位似中心分别为 (

A.2,点$P$
B.$\frac{1}{2}$,点$P$
C.2,点$O$
D.$\frac{1}{2}$,点$O$
D
)
A.2,点$P$
B.$\frac{1}{2}$,点$P$
C.2,点$O$
D.$\frac{1}{2}$,点$O$
答案:
7.D
8. 如图,已知$D$,$E$分别是$\triangle ABC$的边$AB$,$AC$上的点,$DE // BC$,且$S_{\triangle ADE}:S_{四边形DBCE} = 1:8$,那么$AE:AC$等于 (
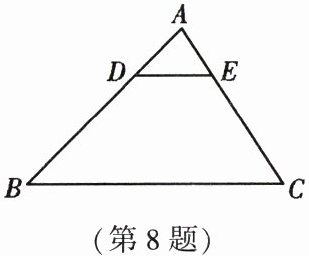
A.$1:9$
B.$1:3$
C.$1:8$
D.$1:2$
B
)
A.$1:9$
B.$1:3$
C.$1:8$
D.$1:2$
答案:
8.B
9. 如图,在$□ ABCD$中,$AE:ED = 1:2$,$S_{\triangle AEF} = 6cm^{2}$,则$S_{\triangle CBF}$等于 (
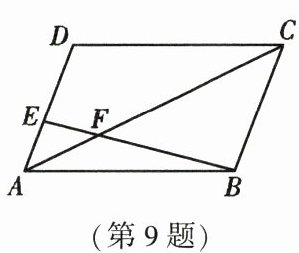
A.$12cm^{2}$
B.$24cm^{2}$
C.$54cm^{2}$
D.$15cm^{2}$
C
)
A.$12cm^{2}$
B.$24cm^{2}$
C.$54cm^{2}$
D.$15cm^{2}$
答案:
9.C
10. 如图,点$A$在线段$BD$上,在$BD$的同侧作等腰直角三角形$ABC$和等腰直角三角形$ADE$,$CD$与$BE$,$AE$分别交于点$P$,$M$。有下列结论:①$\triangle BAE \backsim \triangle CAD$;②$MP · MD = MA · ME$;③$2CB^{2} = CP · CM$。其中正确的是 (

A.①②③
B.①
C.①②
D.②③
A
)
A.①②③
B.①
C.①②
D.②③
答案:
10.A
查看更多完整答案,请扫码查看


