《2025年基础训练大象出版社九年级数学全一册北师大版》

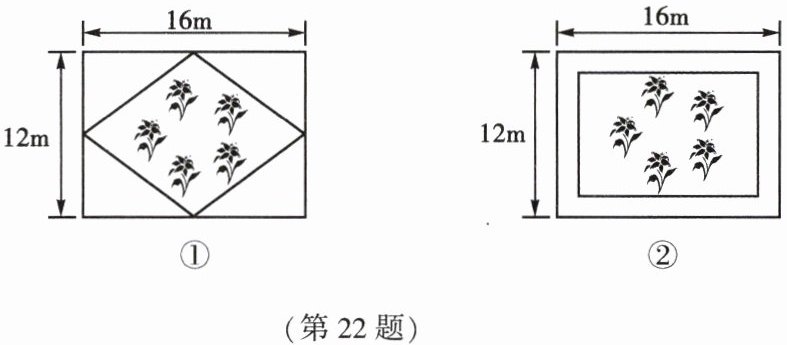
22. (11 分)在一块长为 $16m$、宽为 $12m$ 的矩形荒地上建造一个四边形花圃.
小华提出方案：如图①，取矩形荒地四边中点，顺次相连得到四边形花圃.
小芳提出方案：如图②，在中间建矩形花圃，面积是该矩形荒地的一半，且四周过道宽度相等.
(1)小华的方案中，花圃的形状是菱形，其面积是96$m^{2}$.
(2)小芳的方案中，四周的过道宽度应为多少？

答案： 22.
(1)菱形　96
[提示]如题图①，取矩形荒地四边中点，顺次相连得到四边形花圃是菱形，且菱形的对角线的长分别为$12m$和$16m$，
　故$S_ {菱形} = \frac {1} {2} × 12 × 16 = 96(m^ {2})$.
(2)设过道宽度均为$xm$，根据题意，得
　$(16 - 2x)(12 - 2x) = \frac {1} {2} × 16 × 12$，
　解这个方程，得$x _ {1} = 2,x _ {2} = 12$.
　但$x _ {2} = 12$不符合题意，应舍去，
∴$x = 2$.
∴　小芳的方案中，四周的过道宽度应为$2m$.

23. (13 分)探究问题：
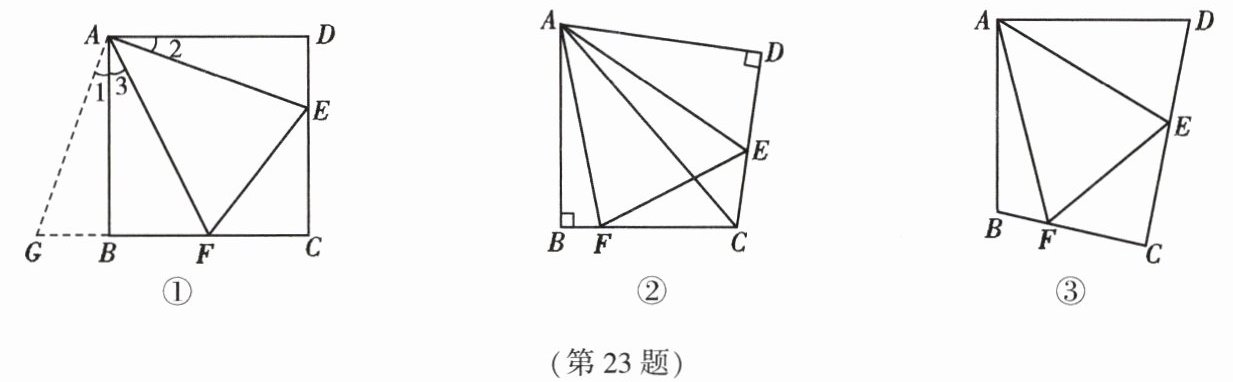
(1)方法感悟：如图①，在正方形 $ABCD$ 中，$E$，$F$ 分别为 $DC$，$BC$ 上的点，且满足 $\angle EAF = 45^{\circ}$，连接 $EF$，求证：$DE + BF = EF$.
感悟解题方法，并完成下列填空：
将 $\triangle ADE$ 绕点 $A$ 顺时针旋转 $90^{\circ}$ 得到 $\triangle ABG$，此时 $AB$ 与 $AD$ 重合.
$\therefore AB = AD$，$BG = DE$，$\angle 1 = \angle 2$，$\angle ABG = \angle D = 90^{\circ}$.
$\therefore \angle ABG + \angle ABF = 90^{\circ}+90^{\circ}=180^{\circ}$，$\therefore G$，$B$，$F$ 三点在同一条直线上.
$\because \angle EAF = 45^{\circ}$，$\therefore \angle 2 + \angle 3 = \angle BAD - \angle EAF = 90^{\circ}-45^{\circ}=45^{\circ}$.
$\because \angle 1 = \angle 2$，$\therefore \angle 1 + \angle 3 = 45^{\circ}$，即 $\angle GAF =$\angle EAF.
又 $\because AG = AE$，$AF = AF$，$\therefore \triangle GAF\cong$\triangle EAF.
$\therefore$GF$= EF$，故 $DE + BF = EF$.
(2)方法迁移：如图②，将 $Rt\triangle ABC$ 沿斜边翻折得到 $\triangle ADC$，$E$，$F$ 分别为 $DC$，$BC$ 边上的点，且 $\angle EAF = \frac{1}{2}\angle DAB$. 试猜想 $DE$，$BF$，$EF$ 之间有何数量关系，并证明你的猜想.
(3)问题拓展：如图③，在四边形 $ABCD$ 中，$AB = AD$，$E$，$F$ 分别为 $DC$，$BC$ 边上的点，满足 $\angle EAF = \frac{1}{2}\angle DAB$. 试猜想当 $\angle B$ 与 $\angle D$ 满足什么关系时，可使 $DE + BF = EF$. 请直接写出你的猜想(不必说明理由).

答案： 23.
(1)$\angle EAF$　$\triangle EAF$　$GF$
(2)$DE + BF = EF$.
证明如下：
假设$\angle DAB$的度数为$m^ {\circ}$，将$\triangle ADE$绕点$A$顺时针旋转$m^ {\circ}$得到$\triangle ABG$，此时$AB$与$AD$重合
∴$AB = AD,BG = DE,\angle GAB = \angle EAD,\angle ABG = \angle D = 90^ {\circ}$.
∴$\angle ABG + \angle ABF = 90^ {\circ} + 90^ {\circ} = 180^ {\circ}$.
∴$G,B,F$三点在同一直线上.
∵$\angle EAF = \frac {1} {2} m^ {\circ}$，
∴$\angle EAD + \angle BAF = \angle BAD - \angle EAF = m^ {\circ} - \frac {1} {2} m^ {\circ} = \frac {1} {2} m^ {\circ}$.
∵$\angle GAB = \angle EAD$，
∴$\angle GAB + \angle BAF = \frac {1} {2} m^ {\circ}$.
∴$\angle GAF = \angle EAF$.
　又
∵$AG = AE,AF = AF$，
∴$\triangle GAF \cong \triangle EAF$.
∴$GF = EF$.
∵$GF = BG + BF = DE + BF$，
∴$DE + BF = EF$.
(3)当$\angle B$与$\angle D$互补时，可使$DE + BF = EF$.