《2025年基础训练大象出版社九年级数学全一册北师大版》

16. （6 分）解方程：$(2x - 3)^{2}=(3x - 2)^{2}$.

答案： 16.移项，得$(2x - 3)^ {2} - (3x - 2)^ {2} = 0$.
　方程左边因式分解，得$(2x - 3 + 3x - 2)(2x - 3 - 3x + 2) = 0$，
　即$5x - 5 = 0$或$-x - 1 = 0$，
　解得$x _ {1} = 1,x _ {2} = - 1$.

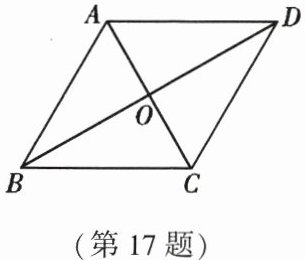
17. （8 分）如图，在 $□ ABCD$ 中，$AC$ 与 $BD$ 相交于点 $O$，已知 $AB = AC = 4$，$\angle ABC = 60^{\circ}$.
（1）求证：四边形 $ABCD$ 是菱形；
（2）求 $BD$ 的长.

答案： 17.
(1)
∵$AB = AC,\angle ABC = 60^ {\circ}$，
∴$\triangle ABC$是等边三角形.
∴$AB = BC$.
∴$□ ABCD$是菱形.
(2)在菱形$ABCD$中，$AC \perp BD,OB = OD$.
∵$AB = AC = 4,\triangle ABC$是等边三角形，
∴$OB = \frac {\sqrt {3}} {2} × 4 = 2 \sqrt {3}$
∴$BD = 2OB = 2 × 2 \sqrt {3} = 4 \sqrt {3}$.

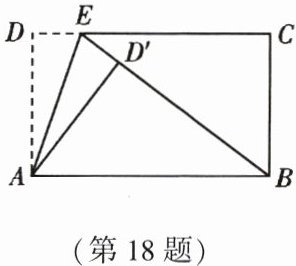
18. （9 分）如图，矩形 $ABCD$ 中，$AD = BC = 6$，$AB = CD = 10$. $E$ 为射线 $DC$ 上的一个动点，$\triangle ADE$ 与 $\triangle AD'E$ 关于直线 $AE$ 对称，当 $\triangle AD'B$ 为直角三角形时，$DE$ 的长是多少？

答案：
18.分两种情况讨论：
　①当点$E$在线段$DC$上时，如图，
∵$\triangle ADE$与$\triangle AD'E$关于直线$AE$对称，
∴$\triangle AD'E \cong \triangle ADE$，
∴$\angle AD'E = \angle D = 90^ {\circ}$.
　
∵$\angle AD'B = 90^ {\circ}$，
∴$\angle AD'B + \angle AD'E = 180^ {\circ}$，
∴$B,D',E$三点共线.
∵$S_ {\triangle ABE} = \frac {1} {2} BE · AD' = \frac {1} {2} AB · AD,AD' = AD$，
∴$BE = AB = 10$.
∵$BD' = \sqrt {AB^ {2} - AD'^ {2}} = \sqrt {10^ {2} - 6^ {2}} = 8$，
∴$DE = D'E = 10 - 8 = 2$.
　②当点$E$在线段$DC$的延长线上时，如图，
　
∵$\angle ABD'' + \angle CBE = \angle ABD'' + \angle BAD'' = 90^ {\circ}$，
∴$\angle CBE = \angle BAD''$
　在$\triangle ABD''$和$\triangle BEC$中，
　$\begin{cases} \angle D'' = \angle BCE, \\ AD'' = BC, \\ \angle BAD'' = \angle CBE, \end{cases}$
∴$\triangle ABD'' \cong \triangle BEC(ASA)$，
∴$BE = AB = 10$.
∵$BD'' = \sqrt {10^ {2} - 6^ {2}} = 8$，
∴$DE = D''E = BD'' + BE = 8 + 10 = 18$.
　综上可知，$DE$的长是$2$或$18$.