第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
22. (12 分)(2023·张家界)2022 年 4 月 21 日《义务教育课程方案和课程标准(2022 年版)》正式颁布,优化了课程设置,其中将劳动教育从综合实践活动课程中独立出来. 某校为了初步了解学生的劳动教育情况,对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间 $x$ 分为如下四组(A:$x < 70$;B:$70\leqslant x < 80$;C:$80\leqslant x < 90$;D:$x\geqslant 90$,单位:分)进行统计,绘制了如下不完整的统计图.
根据以上信息,解答下列问题:
(1)本次抽取的学生有
(2)补全条形统计图.
(3)已知该校九年级有 600 名学生,请估计该校九年级学生中“参加家务劳动的时间”在 80 分钟及以上的学生有多少人.
(4)若 D 组中有 3 名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或画树状图法求抽取的两名同学中恰好是一名女生和一名男生的概率.
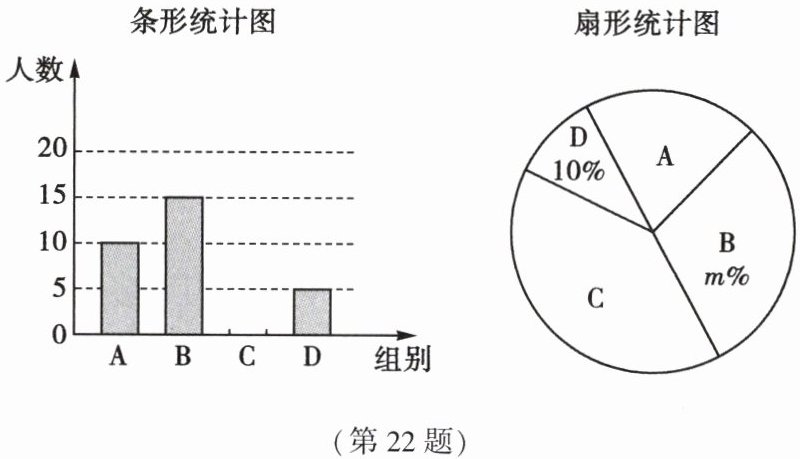
根据以上信息,解答下列问题:
(1)本次抽取的学生有
50
人,扇形统计图中 $m$ 的值为30
.(2)补全条形统计图.
(3)已知该校九年级有 600 名学生,请估计该校九年级学生中“参加家务劳动的时间”在 80 分钟及以上的学生有多少人.
(4)若 D 组中有 3 名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或画树状图法求抽取的两名同学中恰好是一名女生和一名男生的概率.

答案:
22.
(1)50 30
(2)补全条形统计图如下:

(3)$600×\frac{20+5}{50}=300$(人),所以估计该校九年级学生中“参加家务劳动的时间”在80分钟及以上的学生有300人。
(4)若D组中有3名女生,则有2名男生,画树状图如下:
 由图可知,共有20种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有12种,所以抽取的两名同学中恰好是一名女生和一名男生的概率是$\frac{12}{20}$=$\frac{3}{5}$.
由图可知,共有20种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有12种,所以抽取的两名同学中恰好是一名女生和一名男生的概率是$\frac{12}{20}$=$\frac{3}{5}$.
22.
(1)50 30
(2)补全条形统计图如下:

(3)$600×\frac{20+5}{50}=300$(人),所以估计该校九年级学生中“参加家务劳动的时间”在80分钟及以上的学生有300人。
(4)若D组中有3名女生,则有2名男生,画树状图如下:
 由图可知,共有20种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有12种,所以抽取的两名同学中恰好是一名女生和一名男生的概率是$\frac{12}{20}$=$\frac{3}{5}$.
由图可知,共有20种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有12种,所以抽取的两名同学中恰好是一名女生和一名男生的概率是$\frac{12}{20}$=$\frac{3}{5}$. 23. (12 分)甲、乙两人玩数字游戏,先由甲写一个数,再由乙猜甲写的数,要求:他们写和猜的数字只在 1,2,3,4,5 这五个数字中.
(1)请用列表法或画树状图法表示出他们写和猜的所有情况.
(2)如果他们写和猜的数字相同,那么称他们“心灵相通”. 求他们“心灵相通”的概率.
(3)若把甲写的数字记为 $a$,把乙猜的数字记为 $b$,当他们写和猜的数字满足 $|a - b|\leqslant 1$ 时,则称他们“心有灵犀”. 求他们“心有灵犀”的概率.
(1)请用列表法或画树状图法表示出他们写和猜的所有情况.
(2)如果他们写和猜的数字相同,那么称他们“心灵相通”. 求他们“心灵相通”的概率.
(3)若把甲写的数字记为 $a$,把乙猜的数字记为 $b$,当他们写和猜的数字满足 $|a - b|\leqslant 1$ 时,则称他们“心有灵犀”. 求他们“心有灵犀”的概率.
答案:
23.
(1)列表如下:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
(2)根据上表可知,他们写和猜的数字相同的情况有5种,则他们“心灵相通”的概率为$\frac{5}{25}$=$\frac{1}{5}$.
(3)根据把甲写的数字记为$a$,把乙猜的数字记为$b$,当他们写和猜的数字满足$|a - b|\leq1$,那么称他们“心有灵犀”。
满足条件的事件是$|a - b|\leq1$,可以列举出所有满足条件的事件:
①若$a = 1$,则$b = 1,2$;②若$a = 2$,则$b = 1,2,3$;③若$a = 3$,则$b = 2,3,4$;④若$a = 4$,则$b = 3,4,5$;⑤若$a = 5$,则$b = 4,5$.
综上可知,共有$2 + 3 + 3 + 3 + 2 = 13$(种)结果,
故他们“心有灵犀”的概率为$\frac{13}{25}$.
(1)列表如下:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
(2)根据上表可知,他们写和猜的数字相同的情况有5种,则他们“心灵相通”的概率为$\frac{5}{25}$=$\frac{1}{5}$.
(3)根据把甲写的数字记为$a$,把乙猜的数字记为$b$,当他们写和猜的数字满足$|a - b|\leq1$,那么称他们“心有灵犀”。
满足条件的事件是$|a - b|\leq1$,可以列举出所有满足条件的事件:
①若$a = 1$,则$b = 1,2$;②若$a = 2$,则$b = 1,2,3$;③若$a = 3$,则$b = 2,3,4$;④若$a = 4$,则$b = 3,4,5$;⑤若$a = 5$,则$b = 4,5$.
综上可知,共有$2 + 3 + 3 + 3 + 2 = 13$(种)结果,
故他们“心有灵犀”的概率为$\frac{13}{25}$.
查看更多完整答案,请扫码查看


