《2025年基础训练大象出版社九年级数学全一册北师大版》

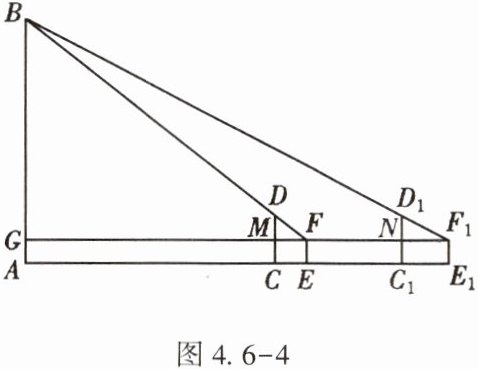
5. (★★)如图4.6-4，为测量学校围墙外直立电线杆AB的高度，小亮在操场上点C处直立高3m的竹竿CD，然后退到点E处，此时恰好看到竹竿顶端D与电线杆顶端B重合；小亮又在点C₁处直立高3m的竹竿C₁D₁，然后退到点E₁处，此时恰好看到竹竿顶端D₁与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m，量得CE=2m，EC₁=6m，C₁E₁=3m.
(1)△FDM∽△FBG，△F₁D₁N∽△F₁BG；
(2)求电线杆AB的高度.

答案： 5.
(1)FBG F₁BG
(2)根据题意，
∵ D₁C₁//BA，
∴ ∠F₁D₁N = ∠F₁BG，∠F₁ND₁ = ∠F₁GB，
∴ △F₁D₁N∽△F₁BG，
∴ $\frac{D₁N}{BG}$ = $\frac{F₁N}{F₁G}$，同理可得△FDM∽△FBG，
∴ $\frac{DM}{BG}$ = $\frac{FM}{FG}$。
∵ D₁N = DM，
∴ $\frac{F₁N}{F₁G}$ = $\frac{FM}{FG}$，即$\frac{3}{GM + 11}$ = $\frac{2}{GM + 2}$，
∴ GM = 16。
∵ $\frac{D₁N}{BG}$ = $\frac{F₁N}{F₁G}$，
∴ $\frac{1.5}{BG}$ = $\frac{3}{27}$，
∴ BG = 13.5，
∴ AB = BG + GA = 15。
答：电线杆AB的高度为15m。

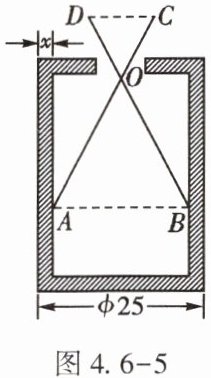
6. (★)如图4.6-5，已知零件的外径为25mm，现用一个交叉卡钳(两条尺长AC和BD相等，OC=OD)量零件的内孔直径AB.若OC:OA=1:2，量得CD=10mm，则零件的厚度x=2.5mm.

答案： 6.2.5

7. (★★)如图4.6-6，一般书本的纸张是由原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依此类推.若各种开本的矩形都相似，那么$\frac{AB}{AD}$等于【 】


A.0.618
B.$\frac{\sqrt{2}}{2}$
C.$\sqrt{2}$
D.2

答案： 7.B

8. (★)我们已经学习和掌握了不少在平地上利用太阳光测量建筑物高度的方法，如果在同一个斜坡上，在同一时刻，测得在斜坡上自己的影子和一棵大树的影子长，那么由自己的身高【 】

A.也能够求出树高
B.还需知道斜坡的角度，才能求出树高
C.不能求出树高
D.只有在光线垂直于斜坡时，才能求出树高

答案： 8.A