《2025年同步测控优化设计九年级物理全一册北师大版》

1. 如图 12 - 3 所示,下列说法正确的是( )。


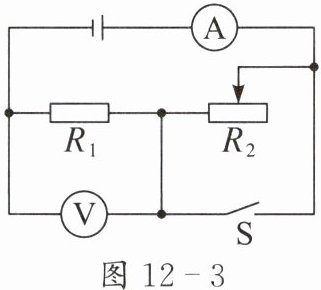
A.断开开关 S,向左移动滑动变阻器$ R_2 $的滑动头,电压表示数与电流表示数的比值变大
B.断开开关 S,向右移动滑动变阻器$ R_2 $的滑动头,电压表示数与电流表示数的比值变小
C.闭合开关 S,电压表示数与电流表示数的比值变大
D.闭合开关 S,电压表示数与电流表示数的比值不变

答案： D

2. 图 12 - 4 为某压力传感器的原理图$,R_1 $为定值电阻,滑动变阻器$ R_2 $的滑动头 P 通过 A、B 间可以伸缩的导线与电路相连,导线位于弹簧内部。闭合开关 S,当压力 F 增大时,下列说法错误的是( )。


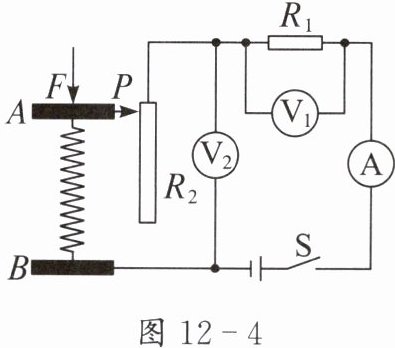
A.电压表$ V_1 $的示数变大
B.电压表$ V_2 $的示数变大
C.电压表$ V_2 $示数与电流表 A 示数的比值变大
D.电压表$ V_1 $示数与电流表 A 示数的比值不变

答案： A

1. 如图 12 - 5 所示,电源电压恒为 6 V。闭合开关 S,电流表$ A_1 $的示数为 0.4 A,电流表$ A_2 $的示数为 0.6 A,则定值电阻$ R_2 $的阻值为_________ Ω。

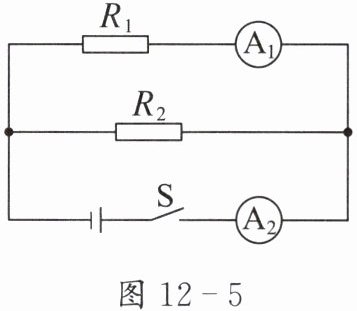
答案： 30

2. 交通运输部门往往通过地磅检测货车载质量情况。图 12 - 6 甲是跨学科学习小组设计的地磅电路原理图,该电路主要由踏板(其所受重力不计)、压力传感器 R、显示承重的仪表(实质为电流表,量程为 0～0.6 A)等组成,电源电压为 12 V,定值电阻 R₀ 的阻值为 5 Ω,压力传感器 R 的阻值与所受压力 F 的关系图像如图 12 - 6 乙所示。

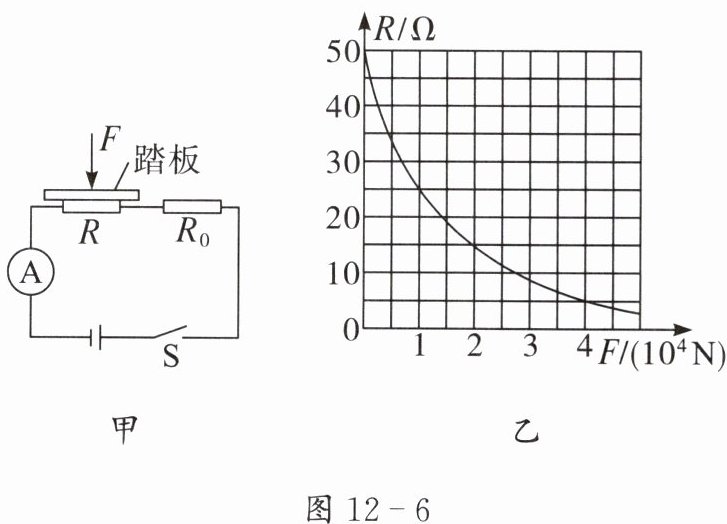
(1)闭合开关 S,当压力传感器 R 的阻值为 35 Ω 时,求电路中的电流。
(2)当电路中的电流为 0.4 A 时,求地磅的测量值(计算出压力传感器 R 所受的压力即可)。
(3)为了使该地磅的最大测量值达到$ 4×10^4 N,$请通过计算写出一种可行的方案。

答案：
(1)0.3 A
(2)1×10⁴ N
(3)见解析
解析
(1)压力传感器R和定值电阻R₀串联,当R=35 Ω时,根据串联电路的电阻规律可得,电路的总电阻$R_{总1}=R+R₀=35 Ω+5 Ω=40 Ω,$电路中的电流$I_{总1}=U/R_{总1}=12 V/40 Ω=0.3 A。$
(2)当电路中的电流为0.4 A时,由欧姆定律可知,电路的总电阻$R_{总2}=U/I_{总2}=12 V/0.4 A=30 Ω,$
此时压力传感器的阻值为$R_{总2}-R₀=30 Ω-5 Ω=25 Ω,$
由题图乙可知,地磅的测量值为1×10⁴ N。
(3)由题图乙可知,当地磅的测量值达到4×10⁴ N时,压力传感器的阻值为5 Ω,
此时电路的总电阻$R_{总最小}=5 Ω+5 Ω=10 Ω,$
由欧姆定律可知电源电压$U_{电源}=I_{最大}R_{总最小}=0.6 A×10 Ω=6 V,$
为了使该地磅的最大测量值达到4×10⁴ N,可将电源电压降至6 V。
本题答案不唯一,合理即可。