《2025年名师学案七年级数学上册沪科版》

11. 按一定规律排列的单项式：$-\frac{1}{4}a^2$,$\frac{1}{8}a^3$,$-\frac{1}{16}a^4$,$\frac{1}{32}a^5$,$-\frac{1}{64}a^6$,…,第100个单项式是$\frac{a^{101}}{2^{101}}$.

答案： $\frac{a^{101}}{2^{101}}$

12. (2023·重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是(B)

A.39
B.44
C.49
D.54

答案： B

13. “腹有诗书气自华,最是书香能放远.”为鼓励和推广全民阅读活动,某书店开展促销活动,促销方法是将原价为$x元的一批图书以0.8(x - 15)$元的价格出售,则下列说法中,能正确表达这批图书的促销方法的是(C)
A.在原价的基础上打8折后再减去15元
B.在原价的基础上打2折后再减去12元
C.在原价的基础上减去15元后再打8折
D.在原价的基础上减去12元后再打8折

答案： C

14. 下列代数式的意义用语言表示错误的是(C)
A.$a^2 - 2ab + b^2表示a$,$b$两数的平方和减去它们乘积的2倍
B.$m + 2n表示m与n$的2倍的和
C.$a^2 + b^2表示a与b$和的平方
D.$(a + b)(a - b)表示a$,$b$两数的和与差的乘积

答案： C

15. 下列结论中,正确的是(D)
A.单项式$\frac{3\pi xy^2}{7}的系数是\frac{3}{7}$,次数是4
B.多项式$2x^2 + xy + 3$是四次三项式
C.单项式$a$的次数是1,系数是0
D.$-xyz^2的系数是-1$,次数是4

答案： D

16. 多项式$3x^{|m|} - (m + 2)x + 7是关于x$的二次三项式,则$m$的值为2.

答案： 2

17. 根据表格,回答问题：

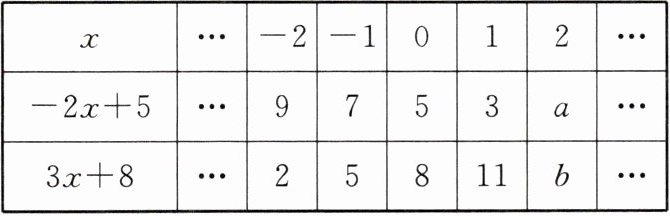
(1)【初步感知】$a = $1,$b = $14；
(2)【归纳规律】
表中$-2x + 5$的值的变化规律是：$x$的值每增加1时,$-2x + 5$的值就减少2.类似地,请写出$3x + 8$的值的变化规律：$x$的值每增加1时,$3x + 8$的值就增加3；
(3)【问题解决】
【新中考·结论开放】请直接写出一个含$x$的代数式,要求$x$的值每增加1,代数式的值就增加5.$5(x-1)$(答案不唯一)

答案： 解:
(1)1 14
(2)2 x的值每增加1时,$3x+8$的值就增加3
(3)$5(x-1)$,答案不唯一.

18. 【新中考·新定义型阅读理解题】定义：若$A - B = n$,则称$A与B是关于数n$的伴随数.比如4与3是关于1的伴随数,$2x - 3与2x是关于-3$的伴随数.
(1)填空：2 022与2023是关于$-1$的伴随数,$-3x+7$与$-3x + 5$是关于2的伴随数；
(2)若$a与2b$是关于5的伴随数,$2b与c$是关于2的伴随数,$c与d$是关于8的伴随数,求$(a - c) + (2b - d) - (2b - c)$的值；
由题意,得$a-2b=5,2b-c=2,c-d=8.(a-c)+(2b-d)-(2b-c)=a-c+2b-d-2b+c=(a-2b)+(2b-c)+(c-d)=5+2+8=15$
(3)已知$A = 8x^2 - 6kx + 13与B = 2(4x^2 - 3x + k)$($k$为常数)始终是关于数$n$的伴随数,求$n$的值.
$A-B=8x^{2}-6kx+13-2(4x^{2}-3x+k)=(6-6k)x+13-2k$,因为A与B始终是关于数n的伴随数,所以$n=(6-6k)x+13-2k$.所以$6-6k=0$,解得$k=1$.所以$n=13-2k=11$

答案： 解:
(1)2023 $-3x+7$
(2)由题意,得$a-2b=5,2b-c=2,c-d=8.(a-c)+(2b-d)-(2b-c)=a-c+2b-d-2b+c=(a-2b)+(2b-c)+(c-d)=5+2+8=15$;
(3)$A-B=8x^{2}-6kx+13-2(4x^{2}-3x+k)=(6-6k)x+13-2k$,因为A与B始终是关于数n的伴随数,所以$n=(6-6k)x+13-2k$.所以$6-6k=0$,解得$k=1$.所以$n=13-2k=11$.