《2025年名师学案七年级数学上册沪科版》

7. 某村种植小麦的面积是 $a\ hm^{2}$,水稻的种植面积是小麦的 $3$ 倍多 $10\ hm^{2}$,则两种农作物一共种植$(4a+10)$$hm^{2}$.

答案： $(4a+10)$

8. 三个连续的偶数,中间一个是 $2n$,其余两个分别为$2n-2$,$2n+2$,这三个数的和是$6n$.

答案： $2n-2$,$2n+2$ $6n$

9. 若 $2x^{2m}y^{3}$ 与 $-5xy^{2n}$ 的和是单项式,则 $|m - n|$ 的值是 (B)
A.$0$
B.$1$
C.$7$
D.$-1$

答案： B

10. 【整体思想】把 $x - 1$ 当作一个整体,合并多项式 $7(x - 1)^{4}-2(x - 1)^{3}-5(x - 1)^{4}-4(x - 1)^{3}$ 中的同类项,结果是$2(x-1)^{4}-6(x-1)^{3}$.

答案： $2(x-1)^{4}-6(x-1)^{3}$

11. 当 $m = $-4时,多项式 $4x^{2}-2xy + y^{2}+mx^{2}$ 中不含 $x^{2}$ 的项.

答案： -4

12. 先化简,再求值：
$a^{3}-a^{2}b + ab^{2}-\frac{1}{2}ab^{2}+\frac{2}{3}a^{3}$,其中 $(a - 1)^{2}+|b - 2| = 0$.

答案： 解:原式$=\frac{5}{3}a^{3}-a^{2}b+\frac{1}{2}ab^{2}$,由题意得$a-1=0$,$b-2=0$,解得$a=1$,$b=2$,当$a=1$,$b=2$时,$\frac{5}{3}a^{3}-a^{2}b+\frac{1}{2}ab^{2}=\frac{5}{3}-2+\frac{1}{2}×1×2^{2}=\frac{5}{3}$.

13. 某窗户的形状如图所示(图中长度单位：$cm$),其中上部是半径为 $x\ cm$ 的半圆形,下部是长为 $y\ cm$ 的长方形.
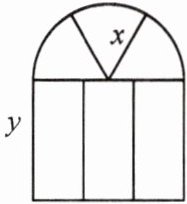
(1)用含 $x$,$y$ 的式子表示窗户外框的总长 $l$；
(2)当 $x = 40$,$y = 120$ 时,求窗户的外框总长 $l$ 的值($\pi$ 取 $3.14$).
]

答案： 解:
(1)$l=\frac{1}{2}×2x\cdot\pi+2x+2y=\pi x+2x+2y$;
(2)当$x=40$,$y=120$时,$l=\pi x+2x+2y\approx40×3.14+2×40+2×120\approx445.6(cm)$

14. 有这样一道题：“当 $a = 0.35$,$b = -0.28$ 时,求多项式 $7a^{3}-6a^{3}b + 3a^{2}b + 3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+2024$ 的值. ”小明说：“本题中 $a = 0.35$,$b = -0.28$ 是多余的条件”；小强马上反对说：“这不可能,多项式中每项都含有 $a$ 和 $b$,不给出 $a$,$b$ 的值怎么能求出多项式的值呢?”你同意哪名同学的观点？请说明理由.

答案： 解:我同意小明的观点.因为$7a^{3}-6a^{3}b+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+2024=(7+3-10)a^{3}+(-6+6)a^{3}b+(3-3)a^{2}b+2024=2024$,所以$a=0.35$,$b=-0.28$是多余的条件,故小明的观点正确.

15. 【新中考·新定义型阅读理解题】如果整式 $A$ 与整式 $B$ 的和为有理数 $a$,那么我们称 $A$,$B$ 为 $a$ 的“友好整式”,例如：$x - 4$ 与 $-x + 5$ 为 $1$ 的“友好整式”；$2ab + 3$ 与 $-2ab + 4$ 为 $7$ 的“友好整式”. 若关于 $x$ 的整式 $2x^{2}+kx + 6$ 与 $-2x^{2}-3x + k - 1$ 为 $n$ 的“友好整式”,求 $n$ 的值.

答案： 解:由题意,得$2x^{2}+kx+6+(-2x^{2}-3x+k - 1)=n$,整理得$(k-3)x+k+5=n$,因为$n$为定值,所以$(k-3)x+k+5$的值与$x$的值无关,所以$k-3=0$,则$k=3$,所以$n=k+5=8$.