第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
6. 若$\vert a\vert = 3$,$\vert b\vert=\frac{1}{3}$,且$a + b\lt0$,则$\frac{a}{b}$的值为(
A.$\pm9$
B.$-9$
C.$\pm1$
D.$-1$
A
)A.$\pm9$
B.$-9$
C.$\pm1$
D.$-1$
答案:
A
7. 有理数$a$,$b$在数轴上的对应点的位置如图所示,则$\frac{a + b}{ab}$的值是(
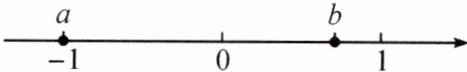
A.负数
B.正数
C.$0$
D.正数或$0$
B
)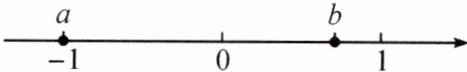
A.负数
B.正数
C.$0$
D.正数或$0$
答案:
B
8. 【分类讨论思想】已知$\vert x\vert = 8$,$\vert y\vert = 2$,且$xy\lt0$,则$\frac{x}{y}$的值为
-4
。
答案:
-4
9. 【教材P40习题T5变式】
(1)$36÷4×(-\frac{1}{4})÷(-\frac{3}{2})$;
(2)$(32\frac{16}{25})÷(-8×4)$。
(1)$36÷4×(-\frac{1}{4})÷(-\frac{3}{2})$;
(2)$(32\frac{16}{25})÷(-8×4)$。
答案:
(1)解:原式=9×(-$\frac{1}{4}$)×(-$\frac{2}{3}$)=$\frac{3}{2}$;
(2)解:原式=(32$\frac{16}{25}$)÷(-32)=(32+$\frac{16}{25}$)×(-$\frac{1}{32}$)=32×(-$\frac{1}{32}$)+$\frac{16}{25}$×(-$\frac{1}{32}$)=-1$\frac{1}{50}$.
(1)解:原式=9×(-$\frac{1}{4}$)×(-$\frac{2}{3}$)=$\frac{3}{2}$;
(2)解:原式=(32$\frac{16}{25}$)÷(-32)=(32+$\frac{16}{25}$)×(-$\frac{1}{32}$)=32×(-$\frac{1}{32}$)+$\frac{16}{25}$×(-$\frac{1}{32}$)=-1$\frac{1}{50}$.
10. 【新中考·新运算型阅读理解题】如果对任何有理数$a$,$b$,定义新运算“$\triangle$”如下:$a\triangle b= \frac{1}{a}÷(-\frac{b}{2})$,如$2\triangle3= \frac{1}{2}÷(-\frac{3}{2})= -\frac{1}{3}$。求$(-2\triangle7)\triangle4$的值。
答案:
解:原式=[(-$\frac{1}{2}$)÷(-$\frac{7}{2}$)]△4=$\frac{1}{7}$△4=1÷$\frac{1}{7}$÷(-$\frac{4}{2}$)=-$\frac{7}{2}$.
11. 已知三个非零有理数$a$,$b$,$c$。
(1)若$\frac{a}{b}\gt0$,则$ab$
(2)若$a + b = 0$,则$\frac{a}{b}=$
(3)若$abc\lt0$,则$a÷ b÷ c$结果的符号为正还是为负?
(4)若$a$,$b$为两个负有理数,当$\frac{a}{b}\lt1$时,判断$a$,$b$的大小关系;
(5)若$a$,$c$为负有理数,$b$为正有理数,求$\frac{a}{\vert a\vert}+\frac{b}{\vert b\vert}+\frac{c}{\vert c\vert}+\frac{abc}{\vert abc\vert}$的值。
(1)若$\frac{a}{b}\gt0$,则$ab$
>
$0$;(填“$\gt$”“$\lt$”或“$=$”);(2)若$a + b = 0$,则$\frac{a}{b}=$
-1
;(3)若$abc\lt0$,则$a÷ b÷ c$结果的符号为正还是为负?
因为abc<0,所以a,b,c中负数的个数是1个或3个,所以a÷b÷c的结果为负数
(4)若$a$,$b$为两个负有理数,当$\frac{a}{b}\lt1$时,判断$a$,$b$的大小关系;
代值法:取a=-1,b=-5,$\frac{a}{b}$=$\frac{-1}{-5}$=$\frac{1}{5}$<1,满足题意,所以a>b
(5)若$a$,$c$为负有理数,$b$为正有理数,求$\frac{a}{\vert a\vert}+\frac{b}{\vert b\vert}+\frac{c}{\vert c\vert}+\frac{abc}{\vert abc\vert}$的值。
由题意得,原式=-1+1+(-1)+1=0
答案:
解:
(1)>
(2)-1
(3)因为abc<0,所以a,b,c中负数的个数是1个或3个,所以a÷b÷c的结果为负数;
(4)代值法:取a=-1,b=-5,$\frac{a}{b}$=$\frac{-1}{-5}$=$\frac{1}{5}$<1,满足题意,所以a>b;
(5)由题意得,原式=-1+1+(-1)+1=0.
(1)>
(2)-1
(3)因为abc<0,所以a,b,c中负数的个数是1个或3个,所以a÷b÷c的结果为负数;
(4)代值法:取a=-1,b=-5,$\frac{a}{b}$=$\frac{-1}{-5}$=$\frac{1}{5}$<1,满足题意,所以a>b;
(5)由题意得,原式=-1+1+(-1)+1=0.
查看更多完整答案,请扫码查看


