《2025年名师学案七年级数学上册沪科版》

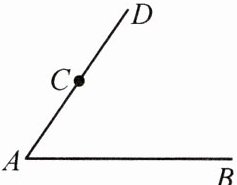
12. (2023·亳州期末)如图,已知 $ ∠BAD $,用直尺和圆规在射线 AD 的右侧作 $ ∠DCP $,使得 $ ∠DCP = ∠BAD $.(不写作法,只需保留作图痕迹)

答案：
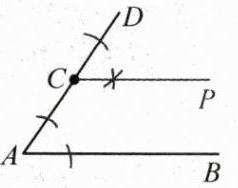
解:如图,∠DCP为所作.

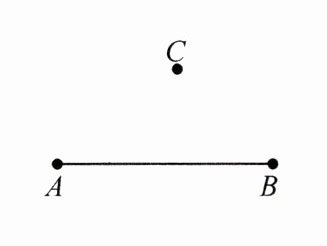
13. (2023·庐江期末)如图,点 C 是线段 AB 外一点,用没有刻度的直尺和圆规画图：
(1)画射线 CB；
(2)画直线 AC；
(3)①延长线段 AB 到 E,使 $ AE = 3AB $；
②在①的条件下,如果 $ AB = 2cm $,那么 $ BE = $______cm.

答案：
解:
(1)如图所示,射线CB即为所求;
(2)如图所示,直线AC即为所求;
(3)①如图所示,线段AE即为所求;②因为AB=2 cm,AE=3AB,所以AE =6 cm.则BE=AE - AB=4 cm.故答案为:4.

14. 已知线段 $ AB = 6cm $,点 C 在直线 AB 上,$ AC = \frac{1}{3}AB $,则 $ BC = $4 cm或8 cm.

答案： 4 cm或8 cm

15. 已知 $ ∠AOB = 3∠BOC $,若 $ ∠BOC = 30^{\circ} $,则 $ ∠AOC = $60°或120°.

答案： 60°或120°

16. 如图,已知数轴上两点 A,B 表示的数分别为 -1,3,点 P 为数轴上的一动点,其表示的数为 x.
(1)$ PA = $|x+1|,$ PB = $|x−3|(用含 x 的式子表示)；
(2)在数轴上是否存在点 P,使 $ PA + PB = 5 $？若存在,请求出 x 的值；若不存在,请说明理由.


存在.因为AB=4,PA+PB=5,所以点P不在点A与点B之间.①当点P在点B右侧时,PA=x+1,PB=x−3,则(x+1)+(x−3)=5,解得x=3.5;②当点P在点A左侧时,PA=−x−1,PB=3−x,则(−x−1)+(3−x)=5,解得x=−1.5.综上所述,在数轴上存在点P,使PA+PB=5,此时x的值为3.5或−1.5.

答案：
(1)|x+1|　　|x−3|　　
(2)存在.因为AB=4,PA+PB=5,所以点P不在点A与点B之间.①当点P在点B右侧时,PA=x+1,PB=x−3,则(x+1)+(x−3)=5,解得x=3.5;②当点P在点A左侧时,PA=−x−1,PB=3−x,则(−x−1)+(3−x)=5,解得x=−1.5.综上所述,在数轴上存在点P,使PA+PB=5,此时x的值为3.5或−1.5.

17. 【新中考·新定义型阅读理解题】射线 OC 是 $ ∠AOB $ 内部的一条射线,若 $ ∠COA = \frac{1}{3}∠AOB $,则我们称射线 OC 是射线 OA 的“友好线”. 例如,如图 1,$ ∠AOB = 60^{\circ} $,$ ∠AOC = ∠COD = ∠BOD = 20^{\circ} $,则 $ ∠AOC = \frac{1}{3}∠AOB $,称射线 OC 是射线 OA 的友好线；同时,由于 $ ∠BOD = \frac{1}{3}∠AOB $,称射线 OD 是射线 OB 的友好线.
【知识运用】
(1)如图 2,$ ∠AOB = 120^{\circ} $,射线 OM 是射线 OA 的友好线,则 $ ∠AOM = $40°；
(2)如图 3,$ ∠AOB = 180^{\circ} $,射线 OC 与射线 OA 重合,并绕点 O 以每秒 $ 2^{\circ} $的速度逆时针旋转,射线 OD 与射线 OB 重合,并绕点 O 以每秒 $ 3^{\circ} $的速度顺时针旋转,当射线 OD 与射线 OA 重合时,运动停止；
①是否存在某个时刻 t(秒),使得 $ ∠COD $ 的度数是 $ 40^{\circ} $,若存在,求出 t 的值,若不存在,请说明理由；
②当射线 OC,OD 相遇后,射线 OC,OD 中恰好有一条射线是另一条射线的友好线,则此时 t 的值是$\frac{540}{13}$秒或45秒.

答案：
(1)40°　
(2)射线OD与射线OA重合时,t=60(秒),①存在某个时刻t(秒),使得∠COD的度数是40°,有两种情况:在OC,OD相遇前,180°−3t°−2t°=40°.解得t=28;在OC,OD相遇后,3t°+2t°−180°=40°.解得t=44.综上所述，当t为28秒或44秒时，∠COD的度数是40°.　　②$\frac{540}{13}$秒或45秒