第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. 如图,若输入 $x$ 的值为 $-1$,则输出 $y$ 的值为 $-1$;若输出 $y$ 的值为 $\frac{1}{3}$,则输入 $x$ 的值是(

A.$1$
B.$-\frac{2}{9}$
C.$1$ 或 $-\frac{2}{9}$
D.无法确定
1
)
A.$1$
B.$-\frac{2}{9}$
C.$1$ 或 $-\frac{2}{9}$
D.无法确定
答案:
A[提示:因为-1>-2,所以把x=-1,y=-1代入y=(2x-a)/3,得-1=(2×(-1)-a)/3,解得a=1,所以y=(2x-1)/3或y=3x+1,所以当输出y的值为1/3时,分两种情况:①当x≥-2时,1/3=(2x-1)/3,解得x=1;②当x<-2时,1/3=3x+1,解得x=-2/9>-2,舍去.所以输出y的值为1/3时,输入x的值是1.]
10. 观察如图所示的程序,若输出的结果为 $5$,则输入的 $x$ 值为(
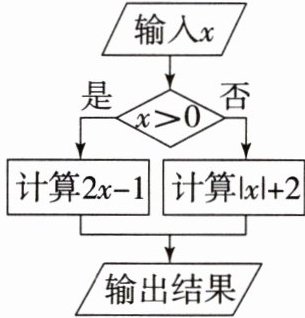
A.$3$
B.$-3$
C.$3$ 或 $-3$
D.$3$ 或 $-1$
C
)
A.$3$
B.$-3$
C.$3$ 或 $-3$
D.$3$ 或 $-1$
答案:
C[提示:当x>0时,因为输出的结果为5,所以2x-1=5,解得x=3;当x<0时,因为输出的结果为5,所以|x|+2=5,所以-x+2=5,解得x=-3.综上,输入的x值为3或-3.]
11. 如图,若开始输入的 $x$ 的值为正整数,最后输出的结果为 $114$,则满足条件的 $x$ 的值为
]

23
。]

答案:
23[提示:若第一个数输出的结果为114,则5x-1=114,解得x=23;若第二个数输出的结果为114,则5(5x-1)-1=114,解得x=4.8(不合题意,舍去).]
12. 方程 $\frac{x}{3× 4} + \frac{x}{4× 5} + \frac{x}{5× 6} + \frac{x}{6× 7} = 4$ 的解为(
A.$x = 30$
B.$x = 24$
C.$x = 21$
D.$x = 12$
21
)A.$x = 30$
B.$x = 24$
C.$x = 21$
D.$x = 12$
答案:
C[提示:x/(3×4)+x/(4×5)+x/(5×6)+x/(6×7)=4,所以x/3-x/4+x/4-x/5+x/5-x/6+x/6-x/7=4,即x/3-x/7=4,去分母,得4x=4×21,解得x=21.]
13. 方程 $\frac{x - 1}{3} + \frac{x - 1}{15} + \frac{x - 1}{35} + \frac{x - 1}{63} + \frac{x - 1}{99} + \frac{x - 1}{143} = 6$ 的解为(
A.$x = 12$
B.$x = 13$
C.$x = 14$
D.$x = 15$
14
)A.$x = 12$
B.$x = 13$
C.$x = 14$
D.$x = 15$
答案:
C[提示:因为(x-1)/3+(x-1)/15+(x-1)/35+(x-1)/63+(x-1)/99+(x-1)/143=6,所以(1/3+1/15+1/35+1/63+1/99+1/143)(x-1)=6,所以1/2×(1-1/3+1/3-1/5+1/5-1/7+1/7-1/9+1/9-1/11+1/11-1/13)(x-1)=6,所以1/2×12/13×(x-1)=6,所以x-1=13,解得x=14.]
14. 在《九章算术》方田章“圆田术”中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这里所用的割圆术所体现的是一种无限与有限的转化思想,比如在 $1 + \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + …$ 中,…“$$”代表按规律不断求和,设 $1 + \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + … = x$。则有 $x = 1 + \frac{1}{2}x$,解得 $x = 2$,故 $1 + \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + … = 2$。类似地,$1 + \frac{1}{5^{2}} + \frac{1}{5^{4}} + \frac{1}{5^{6}} + …$ 的结果为(
A.$\frac{5}{4}$
B.$\frac{25}{24}$
C.$\frac{9}{8}$
D.$2$
B
)A.$\frac{5}{4}$
B.$\frac{25}{24}$
C.$\frac{9}{8}$
D.$2$
答案:
B[提示:设1 + 1/5² + 1/5⁴ + 1/5⁶ + … = x,所以x = 1 + 1/5²x,解得x = 25/24.]
15. 对于两个不相等的有理数 $a,b$,我们规定符号 $\min\{a,b\}$ 表示 $a,b$ 两数中较小的数,例如 $\min\{2,-4\} = -4$,则方程 $\min\{x,-x\} = 3x + 4$ 的解为(
A.$x = -2$
B.$x = -1$
C.$x = -1$ 或 $x = -2$
D.$x = 1$ 或 $x = 2$
-2
)A.$x = -2$
B.$x = -1$
C.$x = -1$ 或 $x = -2$
D.$x = 1$ 或 $x = 2$
答案:
A[提示:当x≥0时,x≥-x,因为min{x,-x}=3x+4,所以-x=3x+4,解得x=-1(-1<0,舍去).当x<0时,x<-x,因为min{x,-x}=3x+4,所以x=3x+4,解得x=-2.综上,方程min{x,-x}=3x+4的解为x=-2.]
16. 对于两个不相等的有理数 $a,b$,我们规定符号 $\max\{a,b\}$ 表示 $a,b$ 两数中较大的数,例如 $\max\{2,4\} = 4$,$\max\{-2,-4\} = -2$。按照这个规定,那么方程 $\max\{x,5x\} = 2x + 6$ 的解为(
A.$x = 2$
B.$x = 3$ 或 $x = -6$
C.$x = 2$ 或 $x = -6$
D.$x = 3$
C
)A.$x = 2$
B.$x = 3$ 或 $x = -6$
C.$x = 2$ 或 $x = -6$
D.$x = 3$
答案:
C[提示:当x>5x时,x=2x+6,解得x=-6.因为5×(-6)=-30,且-6>-30,所以x=-6是该方程的解.当x<5x时,5x=2x+6,解得x=2.因为5×2=10,且2<10,所以x=2是该方程的解.]
查看更多完整答案,请扫码查看


