第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 有 $4$,$-\dfrac{9}{2}$,$-3$,$0$ 四个数,其中最小的是(
A.$4$
B.$-\dfrac{9}{2}$
C.$-3$
D.$0$
B
)A.$4$
B.$-\dfrac{9}{2}$
C.$-3$
D.$0$
答案:
B
2. 已知有理数 $a$,$b$ 在数轴上的对应点的位置如图,则下列结论正确的是(

A.$a > b$
B.$a = b$
C.$b > a$
D.$a = -b$
C
)
A.$a > b$
B.$a = b$
C.$b > a$
D.$a = -b$
答案:
C
3. 如图,数轴上有 $A$,$B$,$C$,$D$ 四个点,其中绝对值最小的数对应的点是(

A.点 $A$
B.点 $B$
C.点 $C$
D.点 $D$
B
)
A.点 $A$
B.点 $B$
C.点 $C$
D.点 $D$
答案:
B[提示:点A,B,C,D在数轴上距离原点越近,其表示的数绝对值越小,所以绝对值最小的数对应的点是B.]
4. 已知有理数 $a$,$b$ 在数轴上的位置如图所示,则 $a$,$b$,$-a$,$-b$ 从大到小的顺序为
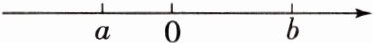
b>−a>a>−b
.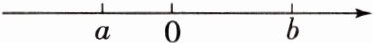
答案:
b>−a>a>−b[提示:在数轴上表示−a,−b如图所示,所以b>−a>a>−b.]
5. 把下列各数在数轴上用点表示出来,并用“$<$”把它们连接起来.
$-3$,$0$,$1\dfrac{1}{2}$,$4.5$,$-1$.
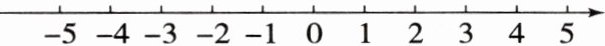
$-3$,$0$,$1\dfrac{1}{2}$,$4.5$,$-1$.
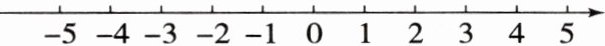
答案:
解:数轴如图,所以−3<−1<0<1$\frac{1}{2}$<4.5.
6. (1)把下列各数在数轴上表示出来,并将它们按照从小到大的顺序用“$<$”连接起来.
$-\dfrac{3}{2}$,$3\dfrac{1}{3}$,$0$,$-4.5$,$5$.
(2)直接写出绝对值小于 $2\dfrac{2}{3}$ 的所有整数.
$-\dfrac{3}{2}$,$3\dfrac{1}{3}$,$0$,$-4.5$,$5$.
(2)直接写出绝对值小于 $2\dfrac{2}{3}$ 的所有整数.
答案:
解:
(1)把各数表示在数轴上如图.故−4.5<−$\frac{3}{2}$<0<3$\frac{1}{3}$<5.
(2)绝对值小于2$\frac{2}{3}$的所有整数为:−2,−1,0,1,2.
(1)把各数表示在数轴上如图.故−4.5<−$\frac{3}{2}$<0<3$\frac{1}{3}$<5.
(2)绝对值小于2$\frac{2}{3}$的所有整数为:−2,−1,0,1,2.
7. 下列各数中比 $0$ 大的是(
A.$-1$
B.$-3.5$
C.$2$
D.$-9$
C
)A.$-1$
B.$-3.5$
C.$2$
D.$-9$
答案:
C
8. (2024·临沂沂水县一模)下列各组数中,大小关系正确的是(
A.$-7 < -5 < -2$
B.$-7 > -5 > -2$
C.$-7 < -2 < -5$
D.$-2 > -7 > -5$
A
)A.$-7 < -5 < -2$
B.$-7 > -5 > -2$
C.$-7 < -2 < -5$
D.$-2 > -7 > -5$
答案:
A[提示:|−7|>|−5|>|−2|,由负数的绝对值越大数越小可知−7<−5<−2.]
9. 下列判断大小正确的是(
A.$-(-0.23) < | -0.32 |$
B.$| -3 | < - | +3 |$
C.$\left| +\dfrac{1}{7} \right| > \left| -\dfrac{1}{6} \right|$
D.$-\left( -\dfrac{1}{2} \right) < -\left( -\dfrac{1}{3} \right)$
A
)A.$-(-0.23) < | -0.32 |$
B.$| -3 | < - | +3 |$
C.$\left| +\dfrac{1}{7} \right| > \left| -\dfrac{1}{6} \right|$
D.$-\left( -\dfrac{1}{2} \right) < -\left( -\dfrac{1}{3} \right)$
答案:
A
10. 用“$>$”“$<$”或“$=$”填空:
(1)$-3$
(2)$-\dfrac{2}{3}$
(1)$-3$
<
$1$;(2)$-\dfrac{2}{3}$
>
$-\dfrac{3}{4}$.
答案:
(1)<
(2)>
(1)<
(2)>
11. 写出一个比 $-1$ 小的有理数为
−2
.
答案:
−2[提示:根据题意,绝对值大于1的负数均可,例如−2 (答案不唯一).]
12. 比较下列各组数的大小:
(1)$-0.3$ 与 $-\dfrac{1}{3}$;
(2)$- | -3 |$ 与 $| -(-3) |$;
(3)$- | -2023 |$ 与 $-(-2024)$;
(4)$-\dfrac{6}{7}$ 与 $-\dfrac{7}{8}$;
(5)$-\left( +\dfrac{2}{3} \right)$ 与 $-\left| -\dfrac{5}{7} \right|$.
(1)$-0.3$ 与 $-\dfrac{1}{3}$;
(2)$- | -3 |$ 与 $| -(-3) |$;
(3)$- | -2023 |$ 与 $-(-2024)$;
(4)$-\dfrac{6}{7}$ 与 $-\dfrac{7}{8}$;
(5)$-\left( +\dfrac{2}{3} \right)$ 与 $-\left| -\dfrac{5}{7} \right|$.
答案:
解:
(1)因为|−0.3|=0.3,|−$\frac{1}{3}$|=$\frac{1}{3}$,而0.3<$\frac{1}{3}$,所以−0.3>−$\frac{1}{3}$.
(2)因为−|−3|=−3,|−(−3)|=3,所以−|−3|<|−(−3)|.
(3)因为−|−2023|=−2023,−(−2024)=2024,所以−|−2023|<−(−2024).
(4)|−$\frac{6}{7}$|=$\frac{48}{56}$,|−$\frac{7}{8}$|=$\frac{49}{56}$,因为$\frac{48}{56}$<$\frac{49}{56}$,所以−$\frac{48}{56}$>−$\frac{49}{56}$,即−$\frac{6}{7}$>−$\frac{7}{8}$.
(5)−(+$\frac{2}{3}$)=−$\frac{2}{3}$,−|−$\frac{5}{7}$|=−$\frac{5}{7}$,|−$\frac{2}{3}$|=$\frac{14}{21}$,|−$\frac{5}{7}$|=$\frac{15}{21}$,因为$\frac{14}{21}$<$\frac{15}{21}$,所以−$\frac{14}{21}$>−$\frac{15}{21}$,即−(+$\frac{2}{3}$)>−|−$\frac{5}{7}$|.
(1)因为|−0.3|=0.3,|−$\frac{1}{3}$|=$\frac{1}{3}$,而0.3<$\frac{1}{3}$,所以−0.3>−$\frac{1}{3}$.
(2)因为−|−3|=−3,|−(−3)|=3,所以−|−3|<|−(−3)|.
(3)因为−|−2023|=−2023,−(−2024)=2024,所以−|−2023|<−(−2024).
(4)|−$\frac{6}{7}$|=$\frac{48}{56}$,|−$\frac{7}{8}$|=$\frac{49}{56}$,因为$\frac{48}{56}$<$\frac{49}{56}$,所以−$\frac{48}{56}$>−$\frac{49}{56}$,即−$\frac{6}{7}$>−$\frac{7}{8}$.
(5)−(+$\frac{2}{3}$)=−$\frac{2}{3}$,−|−$\frac{5}{7}$|=−$\frac{5}{7}$,|−$\frac{2}{3}$|=$\frac{14}{21}$,|−$\frac{5}{7}$|=$\frac{15}{21}$,因为$\frac{14}{21}$<$\frac{15}{21}$,所以−$\frac{14}{21}$>−$\frac{15}{21}$,即−(+$\frac{2}{3}$)>−|−$\frac{5}{7}$|.
查看更多完整答案,请扫码查看


