第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
10. 一列火车正在匀速行驶,它先用 $ 30 $ s 的时间通过了一条长 $ 280 $ m 的桥(即从车头进入桥头到车尾离开桥尾),又用 $ 20 $ s 的时间通过了一条长为 $ 120 $ m 的桥,这列火车的长度是(
A.$ 160 $ m
B.$ 180 $ m
C.$ 200 $ m
D.$ 220 $ m
200
)A.$ 160 $ m
B.$ 180 $ m
C.$ 200 $ m
D.$ 220 $ m
答案:
C[提示:设这列火车的长度是x m,根据题意,得$\frac{280+x}{30}=\frac{120+x}{20}$,解得x=200.所以这列火车的长度是200 m.]
11. 如图,甲、乙两动点分别从正方形 $ ABCD $ 的顶点 $ A $,$ C $ 同时沿正方形的边开始匀速运动. 甲按逆时针方向运动,乙按顺时针方向运动,若乙的速度是甲的 $ 3 $ 倍,则它们第一次相遇在 $ AB $ 边上,它们第 $ 2024 $ 次相遇在(
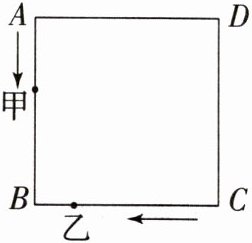
A.$ AB $ 边上
B.$ BC $ 边上
C.$ CD $ 边上
D.$ AD $ 边上
D
)
A.$ AB $ 边上
B.$ BC $ 边上
C.$ CD $ 边上
D.$ AD $ 边上
答案:
D[提示:设甲的速度为v,正方形ABCD的边长为a,甲、乙第2024次相遇的时间为t,则乙的速度为3v.根据题意,得vt+3vt=2a+2023×4a,得$t=\frac{4047a}{2v}$.所以它们第2024次相遇时甲走的路程为$vt=v×\frac{4047a}{2v}=\frac{4047a}{2}$.因为$\frac{4047a}{2}=505×4a+3a+\frac{1}{2}a$,所以它们第2024次相遇在AD边上.]
12. 甲、乙两人跑步,从同一地点出发,沿直线同向而行,甲的速度为 $ 10 $ km/h,乙的速度为 $ 8 $ km/h,乙先出发 $ \dfrac{1}{2} $ h,则甲出发
1或3
h 两人相距 $ 2 $ km.
答案:
1或3[提示:设甲出发x h后,两人相距2 km,则此时乙出发$(x+\frac{1}{2})$h.当甲在乙的前面时,根据题意,得$10x-8(x+\frac{1}{2})=2$,解得x=3;当甲在乙的后面时,根据题意,得$8(x+\frac{1}{2})-10x=2$,解得x=1.综上,甲出发1 h或3 h两人相距2 km.]
13. 小然和小田在 $ 400 $ m 环形跑道上练习跑步,已知小然的速度为每秒钟 $ 4 $ m,小田的速度比小然快 $ \dfrac{1}{2} $,两人同时同地出发,经过
200或40
s 两人第一次相遇.
答案:
200或40[提示:因为小然的速度为每秒钟4 m,小田的速度比小然快$\frac{1}{2}$,则小田的速度为每秒钟6 m.设经过x s,两人第一次相遇,根据题意,得①若两人方向相同,此时6x-4x=400,解得x=200;②若两人方向相反,此时6x+4x=400,解得x=40.综上,经过200 s或40 s两人第一次相遇.]
14. 甲、乙两港口相距 $ 80 $ km,一艘轮船从甲港口逆流向乙港口航行速度为 $ 48 $ km/h,水流速度为 $ 2 $ km/h. 现计划在甲、乙两港口之间修建一个丙港口,若该轮船从甲港口航行到丙港口所用时间与从乙港口航行到丙港口所用时间相同,求甲港口到丙港口之间的距离.
答案:
解:设甲港口到丙港口之间的距离为x km,因为逆流速度为48 km/h,水流速度为2 km/h,所以顺流速度为48+2+2=52(km/h).根据题意,得$\frac{x}{48}=\frac{80-x}{52}$,解得x=38.4.答:甲港口到丙港口之间的距离为38.4 km.
15. 王力和李刚相约去学校 $ 400 $ m 的椭圆形跑道上练习跑步,两人站在同一起跑线上,已知王力每秒钟跑 $ 8 $ m,李刚每秒钟跑 $ 6 $ m(选择其中一个,列方程解决问题)
(1)逆向而行起跑后,多少秒时王力会与李刚再次相迎?
(2)同向而行起跑后,多少秒时王力比李刚多跑一圈?
(1)逆向而行起跑后,多少秒时王力会与李刚再次相迎?
(2)同向而行起跑后,多少秒时王力比李刚多跑一圈?
答案:
(1)设x s时王力会与李刚再次相迎,根据题意,得8x+6x=400,解得$x=\frac{200}{7}$.答:$\frac{200}{7}$s时王力会与李刚再次相迎.
(2)设x s时王力比李刚多跑一圈,根据题意,得8x-6x=400,解得x=200.答:200 s时王力比李刚多跑一圈.
(1)设x s时王力会与李刚再次相迎,根据题意,得8x+6x=400,解得$x=\frac{200}{7}$.答:$\frac{200}{7}$s时王力会与李刚再次相迎.
(2)设x s时王力比李刚多跑一圈,根据题意,得8x-6x=400,解得x=200.答:200 s时王力比李刚多跑一圈.
16. 一架飞机在两城之间飞行,无风时的飞行速度为 $ 552 $ km/h,在一次往返飞行中,顺风飞行用了 $ 5.5 $ h,逆风飞行用了 $ 6 $ h,求:
(1)这次飞行时的风速;
(2)两城之间的航程.
(1)这次飞行时的风速;
(2)两城之间的航程.
答案:
(1)设飞行时的风速为x km/h,则顺风时飞机的航速为(552+x)km/h,逆风时飞机的航速为(552-x)km/h.根据题意,得5.5(552+x)=6(552-x),解得x=24.答:这次飞行时的风速为24 km/h.
(2)两城之间的航程为6(552-24)=6×528=3168(km).答:两城之间的航程为3168 km.
(1)设飞行时的风速为x km/h,则顺风时飞机的航速为(552+x)km/h,逆风时飞机的航速为(552-x)km/h.根据题意,得5.5(552+x)=6(552-x),解得x=24.答:这次飞行时的风速为24 km/h.
(2)两城之间的航程为6(552-24)=6×528=3168(km).答:两城之间的航程为3168 km.
17. 一辆卡车从 $ A $ 地出发匀速开往 $ B $ 地,速度为 $ 40 $ km/h,卡车出发两小时后,一辆出租车从 $ B $ 地出发匀速开往 $ A $ 地,卡车出发 $ 6 $ h,两车同时到达各自的目的地(到达目的地后两车都停止行驶).
解答下列问题:
(1)出租车的速度为
(2)用含 $ x $(行驶的时间)的代数式表示两车行驶的路程之和;
(3)当两车相距 $ 180 $ km 时,求卡车行驶的时间.
解答下列问题:
(1)出租车的速度为
60
km/h;(2)用含 $ x $(行驶的时间)的代数式表示两车行驶的路程之和;
出租车未出发时(即当0≤x≤2),路程和为40x km;出租车出发后(即当2<x≤6),路程和为40x+60(x-2)=(100x-120)(km).答:两车行驶的路程之和为40x km或(100x-120)km.
(3)当两车相距 $ 180 $ km 时,求卡车行驶的时间.
出租车未出发时:根据题意,得40x=240-180,解得x=1.5.出租车出发后:根据题意,得100x-120=240+180,解得x=5.4.答:卡车行驶的时间为1.5 h或5.4 h.
答案:
(1)60
(2)出租车未出发时(即当0≤x≤2),路程和为40x km;出租车出发后(即当2<x≤6),路程和为40x+60(x-2)=(100x-120)(km).答:两车行驶的路程之和为40x km或(100x-120)km.
(3)出租车未出发时:根据题意,得40x=240-180,解得x=1.5.出租车出发后:根据题意,得100x-120=240+180,解得x=5.4.答:卡车行驶的时间为1.5 h或5.4 h.
(1)60
(2)出租车未出发时(即当0≤x≤2),路程和为40x km;出租车出发后(即当2<x≤6),路程和为40x+60(x-2)=(100x-120)(km).答:两车行驶的路程之和为40x km或(100x-120)km.
(3)出租车未出发时:根据题意,得40x=240-180,解得x=1.5.出租车出发后:根据题意,得100x-120=240+180,解得x=5.4.答:卡车行驶的时间为1.5 h或5.4 h.
查看更多完整答案,请扫码查看


