《2025年全科王同步课时练习七年级数学上册青岛版》

13. 下列是根据等式的性质进行变形,正确的是 (D)
A.若 $ ax = ay $,则 $ x = y $
B.若 $ a - x = b + x $,则 $ a = b $
C.若 $ x = y $,则 $ x - 5 = y + 5 $
D.若 $ \frac{x}{4} = \frac{y}{4} $,则 $ x = y $

答案： D[提示:A中,当a=0时,由ax=ay不能推出x=y;B中,因为a-x=b+x,所以等式两边都加x得a=b+2x;C中,因为x=y,所以x-5=y-5;D中,因为$\frac{x}{4}=\frac{y}{4}$,所以等式两边都乘4得x=y.]

14. 下列变形中,不正确的是 (D)
A.若 $ x = y $,则 $ x + 3 = y + 3 $
B.若 $ - 2x = - 2y $,则 $ x = y $
C.若 $ \frac{x}{m} = \frac{y}{m} $,则 $ x = y $
D.若 $ x = y $,则 $ \frac{x}{m} = \frac{y}{m} $

答案： D[提示:D中,当m=0时,$\frac{x}{m}$与$\frac{y}{m}$无意义.]

15. 下列运用等式的性质对等式进行的变形中,错误的是 (A)
A.若 $ a = b $,则 $ \frac{a}{c} = \frac{b}{c} $
B.若 $ a = b $,则 $ ac = bc $
C.若 $ a(x^{2} + 1) = b(x^{2} + 1) $,则 $ a = b $
D.若 $ x = y $,则 $ x - 3 = y - 3 $

答案： A[提示:若a=b,只有c≠0时,$\frac{a}{c}=\frac{b}{c}$成立,所以选项A符合题意;若a=b,则ac=bc,所以选项B不符合题意;若a(x²+1)=b(x²+1),则a=b,所以选项C不符合题意;若x=y,则x-3=y-3,所以选项D不符合题意.]

16. 中央电视台某节目中,有一期的节目如图,两个天平都平衡,则与 1 个球体相等质量的正方体的个数为 (C)


A.4
B.3
C.2
D.1

答案： C[提示:设球体、正方体、圆锥的质量分别为a,b,c.根据题意,得2a=4c,2b=2c.将2a=4c的两边同时除以2,得a=2c.因为2b=2c,所以a=2b.]

17. 如果 $ a = b $,那么 $ \frac{a}{c - 1} = \frac{b}{c - 1} $ 成立时 $ c $ 应满足的条件是c≠1.

答案： c≠1

18. 下列等式变形：①若 $ a = b $,则 $ a + x = b + x $；②若 $ ax = - ay $,则 $ x = - y $；③若 $ 4a = 3b $,则 $ 4a - 3b = 1 $；④若 $ \frac{a}{b} = \frac{3}{4} $,则 $ 4a = 3b $；⑤若 $ \frac{2x}{m} = \frac{3y}{m} $,则 $ 2x = 3y $. 其中一定正确的是①④⑤.(填正确的序号)

答案： ①④⑤

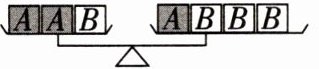
19. 如图,天平两边盘中标有相同字母的物体的质量相同,若 $ A $ 物体的质量为 20 克,当天平处于平衡状态时,$ B $ 物体的质量为10克.

答案： 10克[提示:由图可得2A+B=A+3B,利用等式的性质两边同时减去(A+B),得A=2B,且A的质量为20克,所以B的质量为10克.]

20. 已知 $ 2(3a - b) - 3(a - 2b) = 5 $,求 $ 1 - 9a - 12b $ 的值.

答案： 解:因为2(3a-b)-3(a-2b)=5,所以6a-2b-3a+6b=5,即3a+4b=5.所以1-9a-12b=1-3(3a+4b)=1-3×5=-14.

21. 观察以下等式：
① $ 9 × 9 = 81 = (9 - 1) × 10 + (10 - 9) $；
② $ 9 × 8 = 72 = (8 - 1) × 10 + (10 - 8) $；
③ $ 9 × 7 = 63 = (7 - 1) × 10 + (10 - 7) $；
……
按照以上规律,解决下列问题：
(1) 请再写出一个等式：9×6=54=(6-1)×10+(10-6).
(2) 数学活动课上,王老师给学生变了一个魔术,他让学生任意想一个两位数,然后用这个两位数减去十位数字和个位数字,再将所得差的个位数字与十位数字相加,王老师便能猜中最后的结果.
①王老师猜的结果是：9.
②若设最初想的两位数的十位数字是 $ a $,个位数字是 $ b $,你能解释这个魔术的原理吗？
根据题意，得10a+b-a-b=9a=10(a-1)+(10-a)，所以(a-1)+(10-a)=a-1+10-a=9，所以这个魔术的结果是9。

答案： 解:
(1)由题意可得算式9×6=54=(6-1)×10+(10-6)(答案不唯一).
(2)①取数字92,根据题意,得92-9-2=81,8+1=9,所以王老师猜的结果是9. ②根据题意,得10a+b-a-b=9a=10(a-1)+(10-a),所以(a-1)+(10-a)=a-1+10-a=9,所以这个魔术的结果是9.