第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. (2023·江西中考)单项式$-5ab$的系数为
-5
.
答案:
-5
2. (2023·四川乐山中考)计算:$2a - a$的结果为 (
A.$a$
B.$-a$
C.$3a$
D.$1$
A
)A.$a$
B.$-a$
C.$3a$
D.$1$
答案:
A
3. (2023·浙江丽水中考)计算$a^{2}+2a^{2}$的正确结果是 (
A.$2a^{2}$
B.$2a^{4}$
C.$3a^{2}$
D.$3a^{4}$
C
)A.$2a^{2}$
B.$2a^{4}$
C.$3a^{2}$
D.$3a^{4}$
答案:
C
4. (2023·四川宜宾中考)下列计算正确的是 (
A.$4a - 2a = 2$
B.$2ab + 3ba = 5ab$
C.$a + a^{2}= a^{3}$
D.$5x^{2}y - 3xy^{2}= 2xy$
B
)A.$4a - 2a = 2$
B.$2ab + 3ba = 5ab$
C.$a + a^{2}= a^{3}$
D.$5x^{2}y - 3xy^{2}= 2xy$
答案:
B
5. (2023·辽宁沈阳中考)当$a + b = 3$时,代数式$2(a + 2b)-(3a + 5b)+5$的值为
2
.
答案:
2
6. (2024·四川广安中考)若$x^{2}-2x - 3 = 0$,则$2x^{2}-4x + 1 = $
7
.
答案:
7[提示:因为$x^{2}-2x-3=0$,所以$x^{2}-2x=3$,所以$2x^{2}-4x+1=2(x^{2}-2x)+1=2× 3+1=7.$]
7. (2023·重庆中考)在多项式$x - y - z - m - n$(其中$x > y > z > m > n$)中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”.例如:$x - y - |z - m| - n = x - y - z + m - n$,$|x - y| - z - |m - n| = x - y - z - m + n$,…$$.下列说法:
①存在“绝对操作”,使其运算结果与原多项式相等;②不存在“绝对操作”,使其运算结果与原多项式之和为$0$;③所有的“绝对操作”共有$7$种不同运算结果.
其中正确的个数是 (
A.$0$
B.$1$
C.$2$
D.$3$
①存在“绝对操作”,使其运算结果与原多项式相等;②不存在“绝对操作”,使其运算结果与原多项式之和为$0$;③所有的“绝对操作”共有$7$种不同运算结果.
其中正确的个数是 (
C
)A.$0$
B.$1$
C.$2$
D.$3$
答案:
C[提示:$|x-y|-z-m-n=x-y-z-m-n$,故说法①正确.要使其运算结果与原多项式之和为0,则运算结果应为$-x+y+z+m+n$,由$x>y>z>m>n$可知,无论怎样添加绝对值符号,结果都不可能出现$-x+y+z+m+n$,故说法②正确.当添加一个绝对值时,共有4种情况,分别是$|x-y|-z-m-n=x-y-z-m-n$;$x-|y-z|-m-n=x-y+z-m-n$;$x-y-|z-m|-n=x-y-z+m-n$;$x-y-z-|m-n|=x-y-z-m+n$.当添加两个绝对值时,共有3种情况,分别是$|x-y|-|z-m|-n=x-y-z+m-n$;$|x-y|-z-|m-n|=x-y-z-m+n$;$x-|y-z|-|m-n|=x-y+z-m+n$.共有7种情况;有两对运算结果相同,故共有5种不同运算结果,故说法③不符合题意.]
8. (2023·重庆中考)如果一个四位自然数$\overline{abcd}的各数位上的数字互不相等且均不为0$,满足$\overline{ab}-\overline{bc}= \overline{cd}$,那么称这个四位数为“递减数”.例如:四位数$4129$,因为$41 - 12 = 29$,所以$4129$是“递减数”;又如:四位数$5324$,因为$53 - 32 = 21\neq24$,所以$5324$不是“递减数”.若一个“递减数”为$\overline{a312}$,则这个数为______;若一个“递减数”的前三个数字组成的三位数$\overline{abc}与后三个数字组成的三位数\overline{bcd}的和能被9$整除,则满足条件的数的最大值是______.
4312
8165
答案:
4312 8165[提示:由题意,得$10a+3-31=12$,解得$a=4$,所以这个数为4312.由题意得,$10a+b-(10b+c)=10c+d$,整理得$10a-9b-11c=d$.一个“递减数”的前三个数字组成的三位数$\overline{abc}$与后三个数字组成的三位数$\overline{bcd}$的和为$100a+10b+c+100b+10c+d=100a+10b+c+100b+10c+10a-9b-11c=110a+101b=99(a+b)+11a+2b$.又因为一个“递减数”的前三个数字组成的三位数$\overline{abc}$与后三个数字组成的三位数$\overline{bcd}$的和能被9整除,所以$\frac{11a+2b}{9}$是整数,且$a≠b≠c≠d$,$1\leqslant a\leqslant 9$,$1\leqslant b\leqslant 9$,$1\leqslant c\leqslant 9$,$0\leqslant d\leqslant 9$,$a=9$时,原四位数可得最大值,此时b只能取0,不符合题意,舍去.当$a=8$时,$b=1$,此时$71-11c=d$,c取9或8或7时,均不符合题意.当c取6时,$d=5$,所以满足条件的数的最大值是8165.]
9. 某商店在甲批发市场以每包$m元的价格进了40$包茶叶,又在乙批发市场以每包$n$元($m > n$)的价格进了同样的$60$包茶叶,如果商家以每包$\frac{m + n}{2}$元的价格卖出这种茶叶,卖完后,这家商店 (
A.盈利了
B.亏损了
C.不盈不亏
D.盈亏不能确定
A
)A.盈利了
B.亏损了
C.不盈不亏
D.盈亏不能确定
答案:
A[提示:根据题意列得在甲批发市场茶叶的利润为$40× (\frac{m+n}{2}-m)=20(m+n)-40m=20n-20m$;在乙批发市场茶叶的利润为$60(\frac{m+n}{2}-n)=30(m+n)-60n=30m-30n$,所以该商店的总利润为$20n-20m+30m-30n=10m-10n=10(m-n)$.因为$m>n$,所以$m-n>0$,即$10(m-n)>0$,则这家商店盈利了.]
10. 现有1张大长方形和3张相同的小长方形卡片,按如图的两种方式摆放,则小长方形的长与宽的差是 (
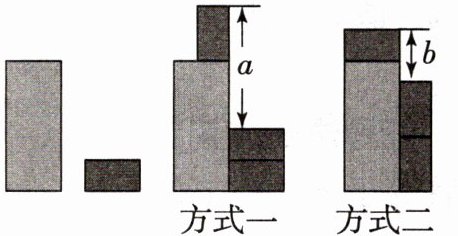
A.$a - b$
B.$\frac{a - b}{2}$
C.$\frac{a - b}{3}$
D.$\frac{a + b}{3}$
C
)
A.$a - b$
B.$\frac{a - b}{2}$
C.$\frac{a - b}{3}$
D.$\frac{a + b}{3}$
答案:
C[提示:设小长方形的长为x,宽为y,大长方形的长为m,则$a+2y=x+m$,$2x+b=y+m$,所以$x=a+2y-m$,$y=2x+b-m$,所以$x-y=(a+2y-m)-(2x+b-m)$,即$x-y=a+2y-m-2x-b+m$,$3x-3y=a-b$,所以$x-y=\frac{a-b}{3}$,即小长方形的长与宽的差是$\frac{a-b}{3}$.]
11. 将四个数a,b,c,d排列成$\begin{vmatrix}a&b\\c&d\end{vmatrix} ,$并且规定$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc,$若$\begin{vmatrix}x + 2&1 - x\\3&2\end{vmatrix} $的值为6,则x的值为 (
A.$1$
B.$5$
C.$-1$
D.$-5$
A
)A.$1$
B.$5$
C.$-1$
D.$-5$
答案:
A[提示:若$\begin{vmatrix} x+2&1-x\\ 3&2\end{vmatrix} =6$,则$2(x+2)-3(1-x)=6$,所以$2x+4-3+3x=6$,所以$x=1$.]
12. 如图,每个字母分别代表不同的数字,四个角上每个三角形的三个顶点上的数字之和都与中间四边形$BDGE$四个顶点上的数字之和相等,若$A = 1$,$C = 3$,$F = 3$,则$H$的值为

5
.
答案:
5[提示:因为$A+B+D=B+D+G+E$,$F+G+D=B+D+G+E$,$G+H+E=B+D+G+E$,$E+B+C=B+D+G+E$,$A=1$,$C=3$,$F=3$,所以$A=G+E=1$①,$F=B+E=3$②,$H=B+D$③,$C=D+G=3$④,②+④,得$B+D+E+G=6$⑤.将①代入⑤,得$B+D=6-1=5$,所以$H=5$.]
13. 阅读材料:我们知道,$2x + 3x - x = (2 + 3 - 1)x = 4x$,类似地,我们把$(a + b)$看成一个整体,则$2(a + b)+3(a + b)-(a + b)= (2 + 3 - 1)(a + b)= 5(a + b)$.“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,请你尝试用此思想解决以下问题:若$a - d = 8$,则$5(a - c)-5(2b - c)+5(2b - d)= $
40
.
答案:
40[提示:$5(a-c)-5(2b-c)+5(2b-d)=5a-5c-10b+5c+10b-5d=5a-5d=5(a-d)$,因为$a-d=8$,所以原式$=5× 8=40$.]
查看更多完整答案,请扫码查看


