《2025年全科王同步课时练习七年级数学上册青岛版》

1. (2023·四川巴中中考)若$x满足x^{2}+3x - 5 = 0$,则代数式$2x^{2}+6x - 3$的值为(B)
A.$5$
B.$7$
C.$10$
D.$-13$

答案： B[提示:由$x^{2}+3x-5=0$,得$x^{2}+3x=5$,所以$2x^{2}+6x-3=2(x^{2}+3x)-3=2×5-3=7.$]

2. (2023·湖南常德中考)若$a^{2}+3a - 4 = 0$,则$2a^{2}+6a - 3$等于(A)
A.$5$
B.$1$
C.$-1$
D.$0$

答案： A[提示:由$a^{2}+3a-4=0$,得$a^{2}+3a=4$,所以$2a^{2}+6a-3=2(a^{2}+3a)-3=2×4-3=5.$]

3. (2023·河南中考)某校计划给每个年级配发$n$套劳动工具,则$3$个年级共需配发$3n$套劳动工具。

答案： $3n$

4. (2023·吉林长春中考)2023长春马拉松于5月21日在南岭体育场鸣枪开跑,某同学参加了7.5公里健康跑项目,他从起点开始以平均每分钟$x$公里的速度跑了10分钟,此时他离健康跑终点的路程为7.5-10x公里。(用含$x$的代数式表示)

答案： $7.5-10x$

5. (2023·临沂中考)观察下列式子：
$1×3 + 1 = 2^{2}$；$2×4 + 1 = 3^{2}$；$3×5 + 1 = 4^{2}$；…。
按照上述规律,$(n-1)(n+1)+1$$=n^{2}$。

答案： $(n-1)(n+1)+1$

6. (2024·四川成都中考)在综合实践活动中,数学兴趣小组对$1\sim n这n$个自然数中,任取两数之和大于$n的取法种数k$进行了探究。发现：当$n = 2$时,只有$\{1,2\}$一种取法,即$k = 1$；当$n = 3$时,有$\{1,3\}和\{2,3\}$两种取法,即$k = 2$；当$n = 4$时,可得$k = 4$；…。若$n = 6$,则$k$的值为9；若$n = 24$,则$k$的值为144。

答案： 9 144[提示:当$n=6$时,从1,2,3,4,5,6中,取两个数的和大于6,这两个数分别是$\{6,1\},\{6,2\},\{6,3\},\{6,4\},\{6,5\},\{5,2\},\{5,3\},\{5,4\},\{4,3\}$,所以$k=5+3+1=9$.当$n=24$时,从1,2,3,$\cdots$,22,23,24中,取两个数的和大于24,这两个数分别是$\{24,1\},\{24,2\},\cdots,\{24,23\},\{23,2\},\{23,3\},\cdots,\{23,22\},\{22,3\},\{22,4\},\cdots,\{22,21\},\cdots,\{14,11\},\{14,12\},\{14,13\},\{13,12\}$.所以$k=23+21+19+\cdots+3+1=144.$]

7. (2023·湖北随州中考)某天老师给同学们出了一道趣味数学题：
设有编号为$1—100的100$盏灯,分别对应着编号为$1—100的100$个开关,灯分为“亮”和“不亮”两种状态,每按一次开关改变一次相对应编号的灯的状态,所有灯的初始状态为“不亮”。现有$100$个人,第$1个人把所有编号是1$的整数倍的开关按一次,第$2个人把所有编号是2$的整数倍的开关按一次,第$3个人把所有编号是3$的整数倍的开关按一次,…,第$100个人把所有编号是100$的整数倍的开关按一次。问最终状态为“亮”的灯共有多少盏？
几位同学对该问题展开了讨论：
甲：应分析每个开关被按的次数找出规律；
乙：$1号开关只被第1个人按了1$次,$2号开关被第1个人和第2个人共按了2$次,$3号开关被第1个人和第3个人共按了2$次……
丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态。
根据以上同学的思维过程,可以得出最终状态为“亮”的灯共有10盏。

答案： 10[提示:因为1号开关被按了1次,2号开关被按了2次,3号开关被按了2次,4号开关被按了3次,5号开关被按了2次,6号开关被按了4次,7号开关被按了2次,8号开关被按了4次,9号开关被按了3次,$\cdots$,所以$n$号开关被按的次数等于$n$的因数的个数,所以因数个数是奇数,故$n$一定是平方数.因为$100=10^{2}$,所以1~100中共有10个平方数,即最终状态为"亮"的灯共有10盏.]

8. (2023·聊城中考)如图,图中数字是从$1$开始按箭头方向排列的有序数阵。从$3$开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对：$(3,5)$,$(7,10)$,$(13,17)$,$(21,26)$,$(31,37)$,…,如果单独把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律。请写出第$n$个数对：______。

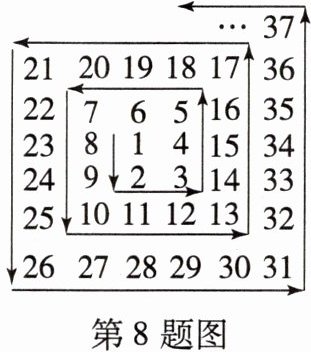
$(n^{2}+n+1,(n+1)^{2}+1)$

答案： $(n^{2}+n+1,(n+1)^{2}+1)$[提示:每个数对的第一个数分别为3,7,13,21,31,$\cdots$,即$1×2+1,2×3+1,3×4+1,4×5+1,5×6+1,\cdots$,则第$n$个数对的第一个数为$n^{2}+n+1$.每个数对的第二个数分别为5,10,17,26,37,$\cdots$,即$2^{2}+1,3^{2}+1,4^{2}+1,5^{2}+1,\cdots$,则第$n$个数对的第二个数为$(n+1)^{2}+1$.所以第$n$个数对为$(n^{2}+n+1,(n+1)^{2}+1)$.]

9. 为开展劳动教育,某校想把一块周长为$30m的长方形荒地按如图方式等距外扩b m$,改造成一个长方形劳动基地,并且用栅栏围起来,则需要栅栏(B)

A.$(30 + 4b)m$
B.$(30 + 8b)m$
C.$4b m$
D.$8b m$

答案： B[提示:由题意得,外扩的长方形周长为$(30+8b)$m.]

10. 某种细菌每分钟分裂成$3$个,一个细菌经过$3$分钟分裂,再继续分裂$t$分钟后共分裂成($3^{3+t}$)
A.$9t$个
B.$9^{t}$个
C.$3^{3t}$个
D.$3^{3 + t}$个

答案： D[提示:因为3分钟分裂了3次,所以再过$t$分钟共分裂$(3+t)$次.又因为每次分裂成3个,所以共分裂成$3^{3+t}$个.]

11. 有如下数列：$a_{1}$,$a_{2}$,$a_{3}$,$a_{4}$,$a_{5}$,$a_{6}$,…,$a_{n - 2}$,$a_{n - 1}$,$a_{n}$,…,满足$a_{n - 2}·a_{n} = 2a_{n - 1}$,已知$a_{1} = 1$,$a_{3} = 4$,则$a_{2024}$的值为(2)
A.$8$
B.$6$
C.$4$
D.$2$

答案： D[提示:因为$a_{n-2}\cdot a_{n}=2a_{n-1}$,所以$2a_{2}=a_{1}\cdot a_{3}$.又因为$a_{1}=1,a_{3}=4$,所以$a_{2}=2$.依次类推,$a_{4}=4,a_{5}=2,a_{6}=1,a_{7}=1,a_{8}=2,\cdots$,由此可见,这列数按1,2,4,4,2,1循环出现.又因为$2024÷6=337\cdots\cdots2$,所以$a_{2024}=2.$]