第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 在圆锥体积公式 $ V = \dfrac{1}{3}\pi r^{2}h $ 中(其中,$ r $ 表示圆锥底面半径,$ h $ 表示圆锥的高),常量与变量分别是 (
A.常量是 $ \dfrac{1}{3},\pi $,变量是 $ V,h $
B.常量是 $ \dfrac{1}{3},\pi $,变量是 $ h,r $
C.常量是 $ \dfrac{1}{3},\pi $,变量是 $ V,h,r $
D.常量是 $ \dfrac{1}{3} $,变量是 $ V,h,\pi,r $
C
)A.常量是 $ \dfrac{1}{3},\pi $,变量是 $ V,h $
B.常量是 $ \dfrac{1}{3},\pi $,变量是 $ h,r $
C.常量是 $ \dfrac{1}{3},\pi $,变量是 $ V,h,r $
D.常量是 $ \dfrac{1}{3} $,变量是 $ V,h,\pi,r $
答案:
C
2. 某人要在规定的时间内加工 100 个零件,如果用 $ n $ 表示工作效率,用 $ t $ 表示规定的时间,下列说法正确的是 (
A.数 100 和 $ n,t $ 都是常量
B.数 100 和 $ n $ 都是变量
C.$ n $ 和 $ t $ 都是变量
D.数 100 和 $ t $ 都是变量
C
)A.数 100 和 $ n,t $ 都是常量
B.数 100 和 $ n $ 都是变量
C.$ n $ 和 $ t $ 都是变量
D.数 100 和 $ t $ 都是变量
答案:
C
3. 超市出售某商品,先在原标价 $ a $ 的基础上提价 20%,再打八折,则商品现售价为 (
A.$ 0.2×(1 + 20\%)a $
B.$ 0.2×(1 - 20\%)a $
C.$ 0.8×(1 + 20\%)a $
D.$ 0.8×(1 - 20\%)a $
C
)A.$ 0.2×(1 + 20\%)a $
B.$ 0.2×(1 - 20\%)a $
C.$ 0.8×(1 + 20\%)a $
D.$ 0.8×(1 - 20\%)a $
答案:
C
4. 一次知识竞赛共有 24 道选择题,规定:答对一道得 3 分,不答或答错一道扣 1 分,如果某位学生答对了 $ x $ 道题,则用式子表示他的成绩为 (
A.$ [3x - (24 + x)] $ 分
B.$ [100 - (24 - x)] $ 分
C.$ 3x $ 分
D.$ [3x - (24 - x)] $ 分
D
)A.$ [3x - (24 + x)] $ 分
B.$ [100 - (24 - x)] $ 分
C.$ 3x $ 分
D.$ [3x - (24 - x)] $ 分
答案:
D
5. 如图,池塘边有一块长为 $ a $ m,宽为 $ b $ m 的长方形土地,现将其余三面都留出宽是 1.5 m 的小路,中间余下的长方形部分做菜地,则菜地的周长为 (
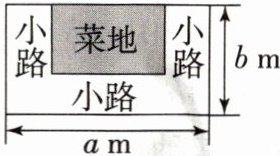
A.$ (a + 2b - 4) $ m
B.$ (a + 2b - 12) $ m
C.$ (2a + 2b - 9) $ m
D.$ (2a + 2b) $ m
C
)
A.$ (a + 2b - 4) $ m
B.$ (a + 2b - 12) $ m
C.$ (2a + 2b - 9) $ m
D.$ (2a + 2b) $ m
答案:
C[提示:因为其余三面都留出宽是1.5m的小路,所以菜地的长为a - 1.5 - 1.5=(a - 3)(m),菜地的宽为(b - 1.5)m,所以菜地的周长为2×(a - 3 + b - 1.5)=(2a + 2b - 9)(m).]
6. 如图,$ A,B $ 两地之间有一条东西走向的道路. 在 $ A $ 地的东边 5 km 处设置第一个广告牌,之后每往东 12 km 就设置一个广告牌. 一辆汽车从 $ A $ 地出发,沿此道路向东行驶. 当经过第 $ n $ 个广告牌时,此车所行驶的路程为
]
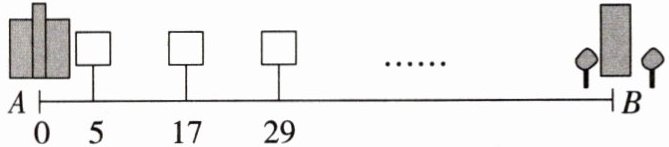
12n - 7
km.]

答案:
(12n - 7)[提示:由题意得,一辆汽车从A地出发,沿此道路向东行驶,当经过第n个广告牌时,此车所行驶的路程为5 + 12(n - 1)=(12n - 7)(km).]
7. 某超市在“元旦”期间进行优惠促销活动,规定一次性购物优惠方案:少于 200 元,不予优惠;高于 200 元但低于 500 元时,九折优惠;消费 500 元或超过 500 元时,其中 500 元部分给予九折优惠,超过 500 元部分给予八折优惠. 根据优惠方案解决下列问题:
(1) 李阿姨一次性购物 650 元,她实际付款多少元?
(2) 李阿姨在该超市一次性购物 $ x $ 元 $ (x > 500) $,她实际付款多少元? (用含 $ x $ 的代数式表示)
(3) 如果李阿姨两次购物货款合计 880 元,第一次购物的货款为 $ a $ 元 $ (200 < a < 350) $,用含 $ a $ 的代数式表示李阿姨两次购物实际付款多少元?
(1) 李阿姨一次性购物 650 元,她实际付款多少元?
(2) 李阿姨在该超市一次性购物 $ x $ 元 $ (x > 500) $,她实际付款多少元? (用含 $ x $ 的代数式表示)
(3) 如果李阿姨两次购物货款合计 880 元,第一次购物的货款为 $ a $ 元 $ (200 < a < 350) $,用含 $ a $ 的代数式表示李阿姨两次购物实际付款多少元?
答案:
解:
(1)由题意得,500×90% + (650 - 500)×80% = 570(元),所以她实际付款570元.
(2)由题意得,500×90% + 80%(x - 500)=(0.8x + 50)(元),所以她实际付款(0.8x + 50)元.
(3)因为第一次购物的货款为a元(200 < a < 350),所以第二次购物的货款超过500元,0.9a + 500×90% + 0.8(880 - a - 500)=0.1a + 754,所以李阿姨两次购物实际付款(0.1a + 754)元.
(1)由题意得,500×90% + (650 - 500)×80% = 570(元),所以她实际付款570元.
(2)由题意得,500×90% + 80%(x - 500)=(0.8x + 50)(元),所以她实际付款(0.8x + 50)元.
(3)因为第一次购物的货款为a元(200 < a < 350),所以第二次购物的货款超过500元,0.9a + 500×90% + 0.8(880 - a - 500)=0.1a + 754,所以李阿姨两次购物实际付款(0.1a + 754)元.
8. 如图,$ y = 3x - 2 $ 表示了自变量 $ x $ 与因变量 $ y $ 的关系,当 $ x $ 每增加 1 时,$ y $ 增加 (
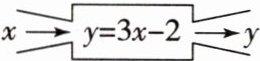
A.1
B.3
C.6
D.12
3
)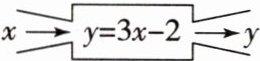
A.1
B.3
C.6
D.12
答案:
B[提示:当x增加1变为x + 1,则y变为3(x + 1)-2 = 3x - 2 + 3.所以当x每增加1时,y增加3.]
9. 如图是一辆汽车行驶的速度 $ (km/h) $ 与时间 $ (min) $ 之间的变化图,下列说法正确的是 (
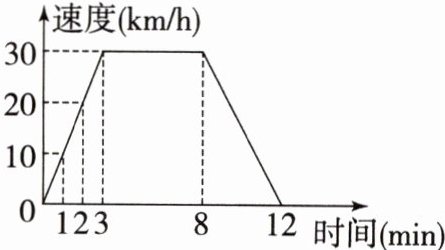
A.时间是因变量,速度是自变量
B.从 3 min 到 12 min,汽车行驶的路程是 150 km
C.时间每增加 1 min,汽车的速度增加 10 km/h
D.第 3 min 时,汽车的速度是 30 km/h
D
)
A.时间是因变量,速度是自变量
B.从 3 min 到 12 min,汽车行驶的路程是 150 km
C.时间每增加 1 min,汽车的速度增加 10 km/h
D.第 3 min 时,汽车的速度是 30 km/h
答案:
D[提示:A中,时间是自变量,速度是因变量;B中,汽车从3 min到8 min行驶的路程是150 km;C中,从3 min到8 min,汽车的速度为30 km/h;D中,第3 min时,汽车的速度是30 km/h.]
查看更多完整答案,请扫码查看


