《2025年全科王同步课时练习七年级数学上册青岛版》

10. 下列说法不正确的是(D)
A.正方形面积公式 $ S = a^{2} $ 中有两个变量
B.圆的面积公式 $ S = \pi r^{2} $ 中的 $ \pi $ 是常量
C.在一个关系式中,用字母表示的量可能不是变量
D.如果 $ a = b $,那么 $ a $,$ b $ 都是常量

答案： D

11.(2023 · 烟台莱州市期末)如图,把两根木条的一端用螺栓固定在一起,木条可自由转动。在转动过程中,下面的量是常量的为(B)

A.$ \angle BAC $ 的度数
B.$ AB $ 的长度
C.$ BC $ 的长度
D.三角形 $ ABC $ 的面积

答案： B[提示:把两根木条的一端用螺栓固定在一起,木条可自由转动,在转动过程中,常量为AB的长度.]

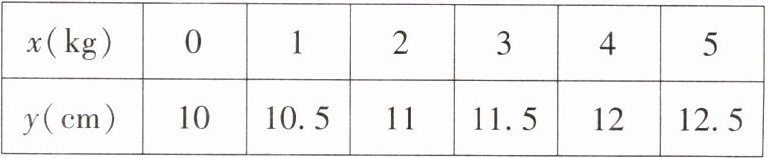
12. 弹簧挂上物体后会伸长,测得一弹簧的长度 $ y $($ cm $)与所挂的物体的质量 $ x $($ kg $)之间有下面的关系：

下列说法正确的是 ①③④。
① $ x $ 与 $ y $ 都是变量；②弹簧不挂重物时的长度为 $ 0 \, cm $；③物体质量每增加 $ 1 \, kg $,弹簧长度增加 $ 0.5 \, cm $；④所挂物体质量为 $ 7 \, kg $ 时,弹簧长度为 $ 13.5 \, cm $。

答案： ①③④[提示:①x与y都是变量,且x是自变量,y是因变量,正确.②弹簧不挂重物时的长度为10cm,错误.③物体质量每增加1kg,弹簧长度增加0.5cm,正确.④所挂物体质量为7kg时,弹簧长度为13.5cm,正确.]

13. 某工厂有一个容积为 $ 280 \, m^{3} $ 的水池,现用 3 台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时抽水 $ 15 \, m^{3} $。
(1) 抽水两个小时后,池中还有水190$ m^{3} $；
(2) 在这一变化过程中哪些是变量？哪些是常量？
在这一变化过程中,水池的容积、抽水机的台数、每台抽水机每小时抽水的体积是常量;抽水时间、水池中的水的体积是变量.

答案：
(1)190；
(2)在这一变化过程中,水池的容积、抽水机的台数、每台抽水机每小时抽水的体积是常量;抽水时间、水池中的水的体积是变量.

14. 周长为 $ 20 \, cm $ 的长方形,若它的一边长是 $ x \, cm $,面积是 $ S \, cm^{2} $。
(1) 请用含 $ x $ 的代数式表示 $ S $,并指出常量与变量；
(2) 当 $ x = 6 $ 时,求 $ S $ 的值。

答案：
(1)S=-x²+10x,周长20cm是常量;一边长x cm,面积S cm²是变量.
(2)24

15. 一汽车油箱里有油 $ 40 \, L $,在行驶过程中,每小时耗油 $ 2.5 \, L $,解答下列问题：
(1) 汽车行驶 $ 1 \, h $ 后油箱里还有油37.5$ L $,汽车行驶 $ 6 \, h $ 后油箱里还有油25$ L $；
(2) 这一变化过程中共有2个变量,其中油箱里剩下的油量和行驶的时间是变量,原油箱油量和每小时耗油的油量是常量；
(3) 设汽车行驶的时间为 $ x \, h $,油箱里剩下的油为 $ Q \, L $,请用含 $ x $ 的式子表示 $ Q $；
$ Q=40-2.5x $
(4) 这辆汽车最多能行驶多少小时？
16h

答案：
(1)37.5；25；
(2)2；油箱里剩下的油量和行驶的时间；原油箱油量和每小时耗油的油量；
(3)Q=40-2.5x；
(4)16h

16. 根据图象回答下列问题。
(1) 图中表示哪两个变量间的关系？
(2) $ A $,$ B $ 两点分别代表了什么？
(3) 请你设计一个实际事例与图中表示的情况一致。
]

答案：
(1)时间与价钱间的关系.
(2)点A表示3日时的价钱为250元,点B表示6日时的价钱为150元.
(3)某个家庭在“五一”长假中每天的消费情况:5月1日花费150元,5月2日花费100元,5月3日花费250元,5月4日花费200元,5月5日花费300元,5月6日花费150元,5月7日花费250元.