《2025年全科王同步课时练习七年级数学上册青岛版》

1. 如果代数式 $2y^{2}-y$ 的值是 $7$,那么代数式 $4y^{2}-2y + 1$ 的值等于(15)
A.$2$
B.$3$
C.$-2$
D.$15$

答案： D[提示:由$2y^{2}-y=7$,得$4y^{2}-2y + 1=2(2y^{2}-y)+1=2×7 + 1=15.]$

2. 若 $3x^{2}+4x + 1 = 0$,则代数式 $6x^{2}+8x + 2024$ 的值是(B)
A.$2021$
B.$2022$
C.$2023$
D.$2024$

答案： B[提示:由$3x^{2}+4x + 1=0$,得$3x^{2}+4x=-1$,故$6x^{2}+8x + 2024=2(3x^{2}+4x)+2024=2×(-1)+2024=2022.]$

3. 当 $x = 2$ 时,代数式 $ax^{3}+2bx - 3$ 的值为 $4$,则 $x = -2$ 时,代数式 $ax^{3}+2bx - 3$ 的值为(-10)
A.$-4$
B.$4$
C.$-10$
D.$-7$

答案： C[提示:由题意得$8a + 4b-3=4$,则$8a + 4b=7$,那么当$x=-2$时,$-8a-4b-3=-(8a + 4b)-3=-7-3=-10.]$

4. 若代数式 $x^{2}-3x + 1$ 的值为 $5$,则代数式 $3 - 2x^{2}+6x$ 的值为-5。

答案： -5[提示:由题意得$x^{2}-3x + 1=5$,即$x^{2}-3x=4$,所以$3-2x^{2}+6x=3-2(x^{2}-3x)=3-2×4=-5.]$

5. 如图,根据流程图中的程序,当输入的数值是$-2$时,则输出的数值为(C)

A.$-8$
B.$-2$
C.$2$
D.$8$

答案： C[提示:当输入的数值是-2时,$-\frac {1}{2}×(-4)=2.]$

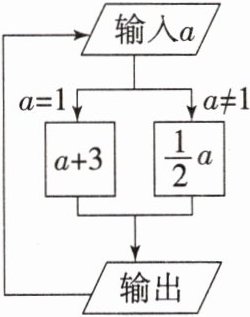
6. 如图是一个运算程序,若第 $1$ 次输入 $a$ 的值为 $16$,则第 $2024$ 次输出的结果是(4)

A.$1$
B.$2$
C.$4$
D.$8$

答案： C[提示:第1次输入a的值为16,则$\frac {1}{2}a=\frac {1}{2}×16=8;$第2次输入a的值为8,则$\frac {1}{2}a=\frac {1}{2}×8=4;$第3次输入a的值为4,则$\frac {1}{2}a=\frac {1}{2}×4=2;$第4次输入a的值为2,则$\frac {1}{2}a=\frac {1}{2}×2=1;$第5次输入a的值为1,则a + 3=1 + 3=4;第6次输入a的值为4,则$\frac {1}{2}a=\frac {1}{2}×4=2;$第7次输入a的值为2,则$\frac {1}{2}a=\frac {1}{2}×2=1;$第8次输入a的值为1,则a + 3=1 + 3=4……所以从第2次开始,输出的结果是4,2,1的循环,因为(2024-1)÷3=674... 1,所以第2024次输出的结果是4.]

7. 按如图程序计算,若开始输入的值为 $x = 3$,则最后输出的结果是(D)

A.$6$
B.$21$
C.$156$
D.$231$

答案： D[提示:当$x=3$时,$\frac {3×(3 + 1)}{2}=6＜100$;当$x=6$时,$\frac {6×(6 + 1)}{2}=21＜100$;当$x=21$时,$\frac {21×(21 + 1)}{2}=231＞100.]$

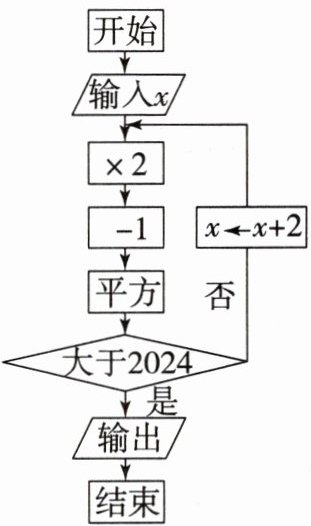
8. 如图是计算机程序的一个流程图,现定义：“$x\leftarrow x + 2$”表示用 $x + 2$ 的值作为 $x$ 的值输入程序再次计算. 比如：当输入 $x = 2$ 时,依次计算作为第一次“传输”,可得 $2×2 = 4$,$4 - 1 = 3$,$3^{2}= 9$,$9$ 不大于 $2024$,所以 $2 + 2 = 4$,把 $x = 4$ 输入程序,再次计算作为第二次“传输”,可得第二次“传输”,可得 $4×2 = 8$,$8 - 1 = 7$,…$$,若输入 $x = 1$,那么经过12次“传输”后可以输出结果,结束程序.
]

答案： 12[提示:每次输入的数应该是1,3,5,7,9,…,第n次输入的数应该是$2n-1$.每次算出的数为$[2(2n-1)-1]^{2}$,由$45^{2}=2025＞2024$,程序结束,可得$2(2n-1)-1=45$,解得$n=12.]$

9. 两列数如下：
$5,7,9,11,13,15,17,19,21……$
$5,8,11,14,17,20,23,26,29……$
这两列数第 $1$ 个相同的数是 $5$,则第 $100$ 个相同的数是(599)
A.$593$
B.$599$
C.$605$
D.$611$

答案： B[提示:第1个相同的数是5,第2个相同的数是$11=5 + 6$,第3个相同的数是$17=5 + 6×2$,第4个相同的数是$23=5 + 6×3$,…,则第n个相同的数是$5 + 6(n-1)=6n-1$,所以第100个相同的数是$6×100-1=599.]$

10. 观察图 $1$、图 $2$、图 $3$ 的运算过程并找出规律,则的值为(B)

A.$8$
B.$-8$
C.$-22$
D.$26$

答案： B[提示:因为$2×(-3)-4=-10$,$-3×(-4)-5=7$,$-4×(-5)-(-6)=26$,所以$-3×5-(-7)=-8.]$

11. 观察下面三行数：
第①行：$2,4,6,8,10,12……$
第②行：$3,5,7,9,11,13……$
第③行：$1,4,9,16,25,36……$
设 $x,y,z$ 分别为第①②③行的第 $100$ 个数,则 $2x - y + z$ 的值为(10199)
A.$10199$
B.$10201$
C.$10203$
D.$10205$

答案： A[提示:观察第①行:2,4,6,8,10,12,…,$2n$,所以第100个数$=2×100=200$,即$x=200$;观察第②行:3,5,7,9,11,13,…,$2n + 1$,所以第100个数$=2×100 + 1=201$,即$y=201$;观察第③行:1,4,9,16,25,36,…,$n^{2}$,所以第100个数$=100^{2}=10000$,即$z=10000$,所以$2x-y + z=2×200-201 + 10000=10199.]$

12. 下面是一组按规律排列的数：$1,2,4,8,16,…$,则第 $2024$ 个数是($2^{2023}$)
A.$2^{2022}$
B.$2^{2023}$
C.$2^{2024}$
D.$2^{2025}$

答案： B[提示:因为$1=2^{0},2=2^{1},4=2^{2},8=2^{3},16=2^{4},…,$所以第n个数可表示为$2^{n-1}(n$为正整数).当n=2024时$,2^{n-1}=2^{2023},$即第2024个数是$2^{2023}.]$