《2025年全科王同步课时练习七年级数学上册青岛版》

9. 已知代数式$x - 2y的值是3$,则代数式$2 - \frac{1}{2}x + y$的值是($\frac{1}{2}$)
A.$-\frac{3}{2}$
B.$-\frac{5}{2}$
C.$\frac{3}{2}$
D.$\frac{1}{2}$

答案： D[提示:由x-2y=3,得原式=2-$\frac{1}{2}$(x-2y)=2-$\frac{3}{2}$=$\frac{1}{2}$.]

10. 如图,是一个运算程序的示意图,若开始输入$x的值为125$,则第$2023$次输出的结果为(1)

A.$1$
B.$5$
C.$25$
D.$125$

答案： A[提示:根据题意得,第一次输出的结果是$\frac{1}{5}$×125=25;第二次输出的结果是$\frac{1}{5}$×25=5;第三次输出的结果是$\frac{1}{5}$×5=1;第四次输出的结果是1+4=5;第五次输出的结果是$\frac{1}{5}$×5=1;第六次输出的结果是1+4=5;第七次输出的结果是$\frac{1}{5}$×5=1;第八次输出的结果是1+4=5;第九次输出的结果是$\frac{1}{5}$×5=1……由此得到规律,从第二次开始奇数次输出的结果为1,偶数次输出的结果为5,所以第2023次输出的结果为1.]

11. 已知$x^{2} - 2x = 1$,则代数式$2025 - 2x + x^{2}$的值为2026。

答案： 2026[提示:由x²-2x=1,得2025-2x+x²=2025+1=2026.]

12. 某面粉加工厂加工甲、乙两种颗粒面粉,每天共加工两种面粉$100$袋,相关信息如下表：

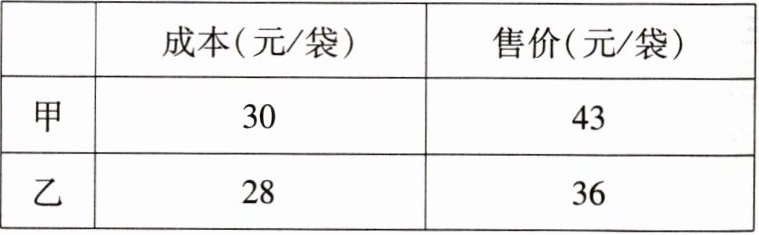
设每天生产甲种颗粒面粉$a$袋。
(1) 每天加工甲、乙两种颗粒面粉的总成本为(2a+2800)元(用含$a$的代数式表示)；
(2) 当$a = 60$时,每天加工甲、乙两种颗粒面粉的总利润为1100元。(利润$=售价-$成本)

答案：
(1)(2a+2800)
(2)1100[提示:已知每天生产甲种颗粒面粉a袋,则每天生产乙种颗粒面粉(100-a)袋.
(1)每天加工甲、乙两种颗粒面粉的总成本为30a+28(100-a)=(2a+2800)(元).
(2)每天加工甲、乙两种颗粒面粉的总利润为(43-30)a+(36-28)(100-a)=(5a+800)(元),当a=60时,总利润为5×60+800=1100(元).]

13. 如图,$AB$是一堵墙(墙足够长),现用$20m$的篱笆围成一个一面靠墙的长方形养鸡场,设养鸡场的宽为$x m$,门的宽为$1m$。
(1) 用含$x$的代数式表示养鸡场的面积；
(2) 当$x = 5$时,求养鸡场的面积。

答案： 解:
(1)已知养鸡场的宽为x m,则它的长为20-2x+1=(21-2x)(m),所以养鸡场的面积是(21-2x)x m².
(2)当x=5时,养鸡场的面积是(21-2x)x=(21-2×5)×5=11×5=55(m²).答:当x=5时,养鸡场的面积是55 m².

14. 为迎接新生,某中学计划添置$100张课桌和x把椅子(x ＞ 100)$。现经调查发现,某家具厂的每张课桌定价$200$元,每把椅子定价$80$元,而厂方在开展促销活动期间,向客户提供了两种优惠方案：
方案一：每买一张课桌就赠送一把椅子；
方案二：课桌和椅子都按定价的$80\%$付款。
(1) 用含$x$的代数式分别表示方案一与方案二各需付款多少元？
(2) 当$x = 300$时,通过计算说明该中学选择上面的两种购买方案哪种更省钱？

答案： 解:
(1)方案一需付款:200×100+80(x-100)=20000+80x-8000=(80x+12000)(元);方案二需付款:200×80%×100+80×80%x=(64x+16000)(元).
(2)当x=300时,方案一需付款:80x+12000=80×300+12000=36000(元),方案二需付款:64x+16000=64×300+16000=35200(元),因为36000＞35200,所以该中学选择方案二更省钱.

15. 如今,网上购物已成为一种新的消费时尚,精品书店想在元旦买一种贺年卡,在互联网上搜索了甲、乙两家网店,已知两家网店的这种贺年卡的质量相同,请阅读相关信息回答问题：
甲网店：贺年卡$1$元/张,运费$8$元,超过$30张全部打6$折；
乙网店：贺年卡$0.8$元/张,运费$8$元,超过$30$张免运费。
(1) 假若精品书店想购买$x$张贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含有$x$的式子表示)？(提示：如需付运费时,运费只需付一次,即$8$元)
(2) 精品书店打算购买$300$张贺年卡,选择哪家网店更省钱？

答案： 解:
(1)当x不超过30时,在甲网店需要花(x+8)元,在乙网店需要花(0.8x+8)元;当x超过30时,在甲网店需要花(0.6x+8)元,在乙网店需要花0.8x元.
(2)当x=300时,甲网店:0.6×300+8=188(元),乙网店:0.8×300=240(元).因为188＜240,所以选择甲网店更省钱.