《2025年全科王同步课时练习七年级数学上册青岛版》

13.元旦在中国也被称为“阳历年”.为庆祝元旦,济南某商场举行促销活动,促销的方法是“消费超过300元时,所购买的商品按原价打八折后,再减50元”.若某商品的原价为x元(x＞300),则活动期间购买该商品实际付的钱数是(A)
A.(80%x-50)元
B.[80%(x-50)]元
C.(50%x-80)元
D.[50%(x-80)]元

答案： A

14.如图,长方形纸片上面有两个
完全相同的灰色长方形,那么
剩余白色长方形的周长为
( D)

A.3b-a
B.3b-2a
C.4b-a
D.4b-2a

答案： D[提示:剩余白色长方形的长为b,宽为(b-a),所以剩余白色长方形的周长=2b+2(b-a)=4b-2a.]

15.已知小明父亲现在的年龄比小明现在的年龄的3倍多2岁,若小明现在的年龄是y岁,则10年后小明父亲的年龄是(3y+12)岁.(用含y的代数式表示)

答案： (3y+12)

16.甲、乙两家超市以相同的价格出售同样的商
品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价八折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价八五折优惠.设顾客预计累计购物x元(x＞300).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用.
(2)小涵准备购买500元的商品,你认为她应该去哪家超市？请说明理由.

答案： 解:
(1)甲超市:300+0.8(x-300)=300+0.8x-240=(0.8x+60)(元);乙超市:200+0.85(x-200)=200+0.85x-170=(0.85x+30)(元).
(2)当x=500时,甲超市:0.8×500+60=460(元);乙超市:0.85×500+30=455(元).因为455＜460,所以她去乙超市更划算.

17.为鼓励人们节约用水,某地实行阶梯式计量水价(如下表所示):

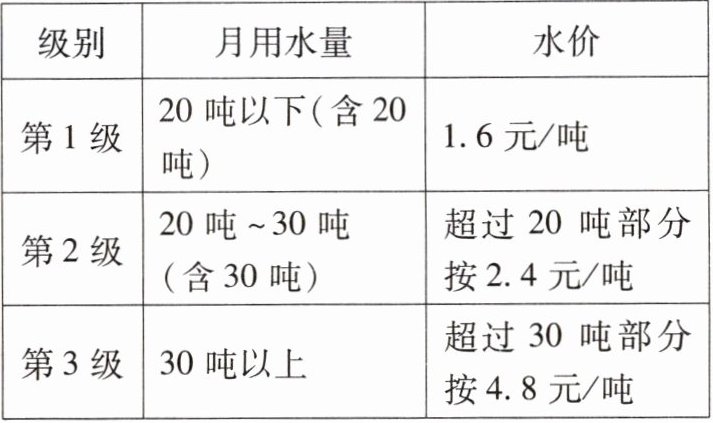
(1)如果某用户某月用水量为10吨,请计算该月需缴水费多少元？
(2)如果某用户某月用水量为27吨,请计算该月需缴水费多少元？
(3)如果某用户某月用水量为m吨(20＜m＜30),则该月需缴水费2.4m-16元(用含m的代数式表示).
(4)如果某用户某月用水量为m吨(m＞30),则该月需缴水费4.8m-88元(用含m的代数式表示).
(1)1.6×10=16(元).答:该月需缴水费16元.
(2)1.6×20+(27-20)×2.4=48.8(元).答:该月需缴水费48.8元.

答案： 解:
(1)1.6×10=16(元).答:该月需缴水费16元.
(2)1.6×20+(27-20)×2.4=48.8(元).答:该月需缴水费48.8元.
(3)1.6×20+(m-20)×2.4=(2.4m-16)(元).
(4)1.6×20+10×2.4+(m-30)×4.8=(4.8m-88)(元).

18.某校组织学生外出研学,旅行社报价每人收费120元,当研学人数超过100时,旅行社给出两种优惠方案:
方案一:研学团队先交1000元后,每人收费100元
方案二:每人收费打九折(九折即原价的90%).
(1)当参加外出研学的总人数是x(x＞100)时,用方案一需花费100x+1000元,用方案二需花费108x元(用含x的式子表示).
(2)当参加外出研学的总人数是200时,采用哪种方案省钱？说说你的理由.
方案一省钱.理由如下:当x=200时,方案一的费用为100×200+1000=21000(元),方案二的费用为108×200=21600(元).因为21600＞21000,所以方案一更省钱.

答案： 解:
(1)方案一的收费为(100x+1000)元;方案二的收费为90%×120x=108x(元).
(2)方案一省钱.理由如下:当x=200时,方案一的费用为100×200+1000=21000(元),方案二的费用为108×200=21600(元).因为21600＞21000,所以方案一更省钱.