《2025年全科王同步课时练习七年级数学上册青岛版》

13. “腹有诗书气自华,最是书香能致远.”为鼓励和推广全民阅读活动,某书店开展促销活动,促销方法是将原价为$x元的一批图书以0.8(x - 15)$元的价格出售,则下列说法中,能正确表达这批图书的促销方法的是 (C)
A.在原价的基础上打八折后再减去$15$元
B.在原价的基础上打二折后再减去$12$元
C.在原价的基础上减去$15$元后再打八折
D.在原价的基础上减去$12$元后再打八折

答案： C[提示:由题意得$0.8(x-15)$是原价减去15元后再打折.]

14. 小咏用现金买了$8$支相同的签字笔,找回了$(50 - 8a)$元,有下列两种说法:
说法Ⅰ:若小咏原有现金$50$元,则每支签字笔$a$元;
说法Ⅱ:若每支签字笔$2a$元,则小咏原有现金$(50 + 8a)$元.
则下面判断正确的是 (C)
A.Ⅰ对Ⅱ错
B.Ⅰ错Ⅱ对
C.Ⅰ与Ⅱ都对
D.Ⅰ与Ⅱ都错

答案： C[提示:每支签字笔的价钱:$50-(50-8a)=8a$,$8a÷8=a$(元);小咏原有现金:$2a×8+50-8a=(50+8a)$(元),所以Ⅰ与Ⅱ都对.]

15. 某轮船顺水航行$3$h,已知轮船在静水中的速度是$a$km/h,水流速度是$b$km/h,轮船共航行$3(a+b)$km.

答案： $3(a+b)$

16. 某种商品原价为每件$p$元,第一次降价每件减少$10$元,第二次降价在第一次降价的基础上每件打八折,则第二次降价后的售价是$0.8(p-10)$元.

答案： $0.8(p-10)$

17. 某水泥仓库一周$7$天内进出水泥的吨数如下 (“+”表示进库,“-”表示出库):$+25$,$-15$,$-22$,$+24$,$-21$,$+14$,$-12$.
(1)经过这$7$天,仓库里的水泥是增多还是减少了? 增多或减少了多少吨?
(2)经过这$7$天,仓库管理员结算发现库里还存$100$吨水泥,那么$7$天前,仓库里存有水泥多少吨?
(3)如果进仓库的水泥装卸费是每吨$a$元,出仓库的水泥装卸费是每吨$b$元,求这$7$天要付多少元装卸费? (用含$a$,$b$的式子表示)

答案： 解:
(1)$+25-15-22+24-21+14-12=-7$,所以经过这7天,仓库里的水泥减少了7吨.
(2)因为$100-(-7)=100+7=107$(吨),所以7天前,仓库里存有水泥107吨.
(3)进仓库的装卸费为$[(+25)+(+24)+(+14)]a=63a$.出仓库的装卸费为$(|-15|+|-22|+|-21|+|-12|)b=70b$.所以这7天要付$(63a+70b)$元装卸费.

18. 某超市出售一种商品,其原价为$a$元,现有三种调价方案:
(1)先提价$20\%$,再降价$20\%$;
(2)先降价$20\%$,再提价$20\%$;
(3)先提价$15\%$,再降价$15\%$.
这三种方案调价结果是否一样? 最后是不是都恢复了原价?

答案： 解:由题意可得,
(1)中的调价结果是$a(1+20\%)(1-20\%)=0.96a$.
(2)中的调价结果是$a(1-20\%)(1+20\%)=0.96a$.
(3)中的调价结果是$a(1+15\%)(1-15\%)=0.9775a$.故前两种方案调价结果一样,最后都没恢复原价.

19. 如图,某影厅共有$16$排座位,第$1排有m$个座位,第$2排比第1排多6$个座位,第$3$排及后面每排座位数相同,都比第$2排多n$个座位.

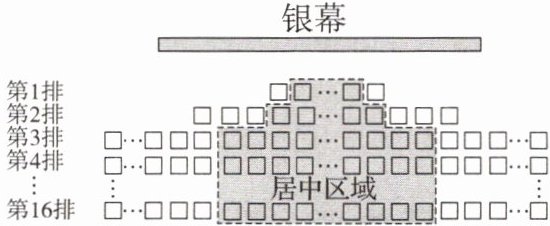
(1)该影厅第$3$排有______个座位(用含$m$,$n$的式子表示);
(2)图中的阴影区域为居中区域,第$1排的两侧各去掉1个座位后得到第1$排的居中区域,第$2排的居中区域比第1排的居中区域在两侧各多1$个座位,第$3$排及后面每排的居中区域座位数相等,都比第$2排的居中区域在两侧各多2$个座位. 居中区域的第$7$,$8$,$9$排为最佳观影位置.
①若该影厅的第$1排有12$个座位,则居中区域的第$2$排有______个座位,居中区域的第$3$排有______个座位;
②若该影厅的最佳观影位置共有$39$个座位,请你用含$n$的式子表示该影厅的座位数.

(1)m+n+6
(2)①1216
②14n+234

答案： 解:
(1)由题知,第2排的座位数为$(m+6)$个,第3排的座位数为$(m+n+6)$个.
(2)①由该影厅的第1排有12个座位得,第1排居中区域的座位数为$12-2=10$(个),第2排居中区域的座位数为$10+2=12$(个),第3排居中区域的座位数为$12+4=16$(个). ②由题知,第1排居中区域的座位数为$(m-2)$个,第2排居中区域的座位数为$m-2+2=m$(个),第3排居中区域的座位数为$(m+4)$个.又因为第3排及后面每排的居中区域座位数相等,所以第7,8,9排的居中区域的座位数都是$(m+4)$个.又因为居中区域的第7,8,9排为最佳观影位置,且该影厅的最佳观影位置共有39个座位,所以$3(m+4)=39$,解得$m=9$,所以第1排的座位数为9个,第2排的座位数为15个,第3排的座位数为$(15+n)$个,故该影厅的座位总数为$9+15+(16-2)(15+n)=14n+234$(个).