《2025年全科王同步课时练习七年级数学上册青岛版》

10. 规定 $a \triangle b = a - 2b$,则 $3 \triangle (-2)$ 的值为(7)
A.$7$
B.$-5$
C.$1$
D.$-1$

答案： A[提示:由题意,得3△(-2)=3-2×(-2)=3+4=7.]

11. 如图,按图中的程序进行计算,如果输入的数是$-2$,那么输出的数是【img】(A)

A.$-50$
B.$50$
C.$-250$
D.$250$

答案： A[提示:-2×(-5)=10,10×(-5)=-50.故输出的数是-50.]

12. 小明和小红利用温差测量山峰的高度. 小明在山顶测得温度是$-1^{\circ}C$,小红此时在山脚测得温度是$11^{\circ}C$,已知该地区高度每增加$100m$,气温大约下降$0.8^{\circ}C$,则这个山峰的高度大约是(1500m)
A.$800m$
B.$1250m$
C.$1200m$
D.$1500m$

答案： D[提示:由题意得[11-(-1)]÷0.8×100=(11+1)÷0.8×100=12÷0.8×100=15×100=1500(m),所以这个山峰的高度大约是1500 m.]

13. 若 $p,q$ 互为倒数,$m,n$ 互为相反数,则 $pq - m - n - 3\frac{1}{3} = $ -$\frac{7}{3}$。

答案： -$\frac{7}{3}$[提示:因为p,q互为倒数,所以pq=1.因为m,n互为相反数,所以m+n=0.所以原式=pq-(m+n)-3$\frac{1}{3}$=1-0-3$\frac{1}{3}$=-$\frac{7}{3}$.]

14. 已知 $x$ 是最大的负整数,$y$ 与比 $x$ 小 $2$ 的数互为相反数,$z$ 是绝对值最小的有理数. 规定一种新运算“※”,两数 $a,b$ 通过“※”运算得 $(a + 2) × 2 - b$,即 $a※b = (a + 2) × 2 - b$,例如:$3※5 = (3 + 2) × 2 - 5 = 10 - 5 = 5$,则 $z※y$ 的值为 1。

答案： 1[提示:由题意,x是最大的负整数,y与比x小2的数互为相反数,z是绝对值最小的有理数,所以x=-1,y=-(-1-2)=3,z=0,所以z※y=(0+2)×2-3=4-3=1.]

15. 计算：
(1) $(-\frac{1}{3} + \frac{1}{2}) × 6 ÷ \vert -\frac{1}{5} \vert$；
(2) $(-1)^{2024} + (-10) ÷ \frac{1}{2} × 2 - [(-3)^{3} - 2]$。

答案：
(1)(-$\frac{1}{3}$+$\frac{1}{2}$)×6÷|-$\frac{1}{5}$|=(-$\frac{2}{6}$+$\frac{3}{6}$)×6÷$\frac{1}{5}$=$\frac{1}{6}$×6×5=5.
(2)(-1)²⁰²⁴+(-10)÷$\frac{1}{2}$×2-[(-3)³-2]=1+(-10)×2×2-(-27-2)=1-40+29=-10.

16. 请根据图中提供的信息,解答下列问题：

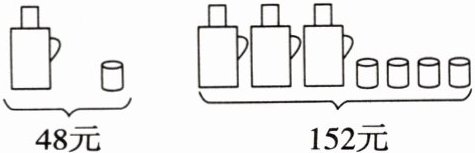
【img】
(1)一个水壶是多少元?
(2)商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水壶赠送两个水杯,另外购买的水杯按原价卖. 某单位想要买 $10$ 个水壶和 $30$ 个水杯,若只在同一家商场购买,那么选择哪家商场购买更合算? 并说明理由.

答案：
(1)48×4-152=192-152=40(元).答:一个水壶是40元.
(2)由
(1)得一个水杯是48-40=8(元),甲商场:(40×10+8×30)×0.8=512(元),乙商场:40×(-$\frac{12}{5}$)+1$\frac{2}{3}$×(-$\frac{12}{5}$)-3.75×(-$\frac{12}{5}$)=-24-4+9=-19.

17. 【概念学习】定义新运算:求若干个相同的有理数(均不等于 $0$)的商的运算叫做除方. 比如 $2 ÷ 2 ÷ 2, (-3) ÷ (-3) ÷ (-3) ÷ (-3)$ 等,类比有理数的乘方,我们把 $2 ÷ 2 ÷ 2$ 写作 $2^{\circledast}$,读作“$2$ 的圈 $3$ 次方”,$(-3) ÷ (-3) ÷ (-3) ÷ (-3)$ 写作 $(-3)^{\circledast}$,读作“$(-3)$ 的圈 $4$ 次方”. 一般地,把 $\underbrace{a ÷ a ÷ a ÷ … ÷ a}_{n个a}$ 记作 $a^{\circledast}$,读作“$a$ 的圈 $n$ 次方”. 特别地,规定:$a^{\circledast} = a$.
【初步探究】
(1) 直接写出计算结果:$2024^{\circledast} =$ 1；
(2) 若 $n$ 为任意正整数,下列关于除方的说法中,正确的有 ABD；(填选项)
A. 任何非零数的圈 $2$ 次方都等于 $1$
B. 任何非零数的圈 $3$ 次方都等于它的倒数
C. 圈 $n$ 次方等于它本身的数是 $1$ 和 $-1$
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?
(3) 请把有理数 $a(a \neq 0)$ 的圈 $n(n \geq 3)$ 次方写成幂的形式:$a^{\circledast} =$ $(\frac{1}{a})^{n-2}$；
(4) 计算: $-1^{\circledast} - 14^{2} ÷ (-\frac{1}{2})^{\circledast} × (-7)^{\circledast}$。
解:原式=-1-196÷4×$\frac{1}{7^{\circledast}}$=-1-49×$\frac{1}{2401}$=-1-$\frac{1}{49}$=-1$\frac{1}{49}$

答案：
(1)1[提示:2024⁽²⁾=2024÷2024=1.]
(2)ABD[提示:A中,因为a⁽²⁾=a÷a=1(a≠0),所以任何非零数的圈2次方都等于1. B中,因为a⁽³⁾=a÷a÷a=$\frac{1}{a}$(a≠0),所以任何非零数的圈3次方都等于它的倒数. C中,圈n次方等于它本身的数是1或-1,说法错误,(-1)⁽²⁾=1. D中,根据新定义以及有理数的乘除法法则可知,负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.]
(3)($\frac{1}{a}$)ⁿ⁻²[提示:a⁽ⁿ⁾=a÷a÷a÷…÷a=a·$\frac{1}{a}$·$\frac{1}{a}$·$\frac{1}{a}$·…·$\frac{1}{a}$=($\frac{1}{a}$)ⁿ⁻².]
(4)解:原式=-1-196÷4×$\frac{1}{7⁽⁴⁾}$=-1-49×$\frac{1}{2401}$=-1-$\frac{1}{49}$=-1$\frac{1}{49}$.