第94页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
1. 用加减消元法将方程组$\begin{cases}5x - 3y = -5, \\ 5x + 4y = -1 \end{cases} 中的未知数x$消去后,得到的方程是(
A.$y = 4$
B.$7y = 4$
C.$-7y = 4$
D.$-7y = 14$
B
)A.$y = 4$
B.$7y = 4$
C.$-7y = 4$
D.$-7y = 14$
答案:
B
2. 在用加减消元法解二元一次方程组$\begin{cases}3x - 2y = 5①, \\ 2x - 3y = 10② \end{cases} $时,经过某个变化可得$5x = -5$,则这个变化是(
A.$①×2 + ②×3$
B.$①×2 - ②×3$
C.$①×3 - ②×2$
D.$①×3 + ②×2$
C
)A.$①×2 + ②×3$
B.$①×2 - ②×3$
C.$①×3 - ②×2$
D.$①×3 + ②×2$
答案:
C
3. 已知$x$,$y满足方程组\begin{cases}x + 2y = 1, \\ 2x + y = 2, \end{cases} 则x + y$的值为(
A.$1$
B.$2$
C.$3$
D.$4$
A
)A.$1$
B.$2$
C.$3$
D.$4$
答案:
A
4. 已知方程组$\begin{cases}x + 3y = 17, \\ 2x - 3y = 6, \end{cases} $只要两个方程两边分别
相加
,就可以消去未知数y
。
答案:
相加 y
5. 方程组$\begin{cases}2x + 3y = 13, \\ 3x - 2y = 0 \end{cases} $的解为
$\left\{\begin{array}{l} x=2,\\ y=3\end{array}\right. $
。
答案:
$\left\{\begin{array}{l} x=2,\\ y=3\end{array}\right. $
6. 解二元一次方程组$\begin{cases}13x - 6y = 25①, \\ 27x - 4y = 19② \end{cases} $时,利用$②×3 - ①×2$消去y后得x =
$\frac {7}{55}$
。
答案:
$\frac {7}{55}$
7. (易错题)(教材 P124 练习第 1 题变式)用加减消元法解下面的二元一次方程组:
(1)$\begin{cases}3x + 2y = 10, \\ 5x - y = 21; \end{cases} $
(2)$\begin{cases}5x + 4y = 6, \\ 2x + 3y = 1. \end{cases} $
(1)$\begin{cases}3x + 2y = 10, \\ 5x - y = 21; \end{cases} $
(2)$\begin{cases}5x + 4y = 6, \\ 2x + 3y = 1. \end{cases} $
答案:
(1)$\left\{\begin{array}{l} 3x+2y=10①,\\ 5x-y=21②,\end{array}\right. $①+②×2,得$13x=52$,解得$x=4$,将$x=4$代入②,得$20-y=21$,解得$y=-1$,故原方程组的解为$\left\{\begin{array}{l} x=4,\\ y=-1\end{array}\right. $
(2)$\left\{\begin{array}{l} 5x+4y=6①,\\ 2x+3y=1②,\end{array}\right. $②×5-①×2,得$7y=-7$,解得$y=-1$,将$y=-1$代入②,得$2x-3=1$,解得$x=2$,故原方程组的解为$\left\{\begin{array}{l} x=2,\\ y=-1\end{array}\right. $
[易错分析]在运用加减消元法解二元一次方程组时,有时需在方程两边同时乘或除以一个非零数时,不能漏掉其中一项.两个方程相加减时,要注意符号,尤其是在减去一个负系数时,要带着前面的性质符号一同计算.
(1)$\left\{\begin{array}{l} 3x+2y=10①,\\ 5x-y=21②,\end{array}\right. $①+②×2,得$13x=52$,解得$x=4$,将$x=4$代入②,得$20-y=21$,解得$y=-1$,故原方程组的解为$\left\{\begin{array}{l} x=4,\\ y=-1\end{array}\right. $
(2)$\left\{\begin{array}{l} 5x+4y=6①,\\ 2x+3y=1②,\end{array}\right. $②×5-①×2,得$7y=-7$,解得$y=-1$,将$y=-1$代入②,得$2x-3=1$,解得$x=2$,故原方程组的解为$\left\{\begin{array}{l} x=2,\\ y=-1\end{array}\right. $
[易错分析]在运用加减消元法解二元一次方程组时,有时需在方程两边同时乘或除以一个非零数时,不能漏掉其中一项.两个方程相加减时,要注意符号,尤其是在减去一个负系数时,要带着前面的性质符号一同计算.
8. (新考法·项目式学习)数学活动课上,小云和小辉在讨论老师出示的一道二元一次方程组的问题:
已知关于$x$,$y的二元一次方程组\begin{cases}3x + 4y = 3①, \\ x + 2y = 2 - 3m② \end{cases} 的解满足2x + 3y = 1③$,求$m$的值。
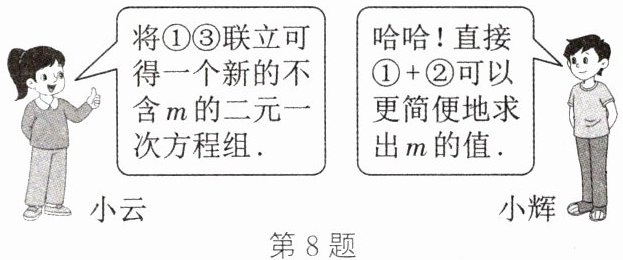
请结合他们如图所示的对话,解答下面的问题:
(1)按照小云的方法,$x$的值为
(2)老师说小辉的方法体现了整体代入的思想,请按照小辉的思路求出$m$的值。
已知关于$x$,$y的二元一次方程组\begin{cases}3x + 4y = 3①, \\ x + 2y = 2 - 3m② \end{cases} 的解满足2x + 3y = 1③$,求$m$的值。

请结合他们如图所示的对话,解答下面的问题:
(1)按照小云的方法,$x$的值为
5
,$y$的值为-3
;(2)老师说小辉的方法体现了整体代入的思想,请按照小辉的思路求出$m$的值。
①+②,得$4x+6y=5-3m$,即$2(2x+3y)=5-3m$,所以$2x+3y=\frac {5-3m}{2}$.因为$2x+3y=1$,所以$\frac {5-3m}{2}=1$,解得$m=1$
答案:
(1)5 -3
(2)①+②,得$4x+6y=5-3m$,即$2(2x+3y)=5-3m$,所以$2x+3y=\frac {5-3m}{2}$.因为$2x+3y=1$,所以$\frac {5-3m}{2}=1$,解得$m=1$
(1)5 -3
(2)①+②,得$4x+6y=5-3m$,即$2(2x+3y)=5-3m$,所以$2x+3y=\frac {5-3m}{2}$.因为$2x+3y=1$,所以$\frac {5-3m}{2}=1$,解得$m=1$
查看更多完整答案,请扫码查看


