《2025年通城学典课时作业本七年级数学上册湘教版》

1. 从 2 开始,连续的偶数相加,它们的和的情况如下：

(1)当$n$个连续的偶数相加时,它们的和$S与n$之间有什么样的关系？用公式表示出来。
(2)按此规律计算：
①$2 + 4 + 6 + … + 300$；
②$162 + 164 + 166 + … + 400$。

答案： （1）由题意易得S=n(n+1) （2）①2+4+6+…+300=150×(150+1)=22 650 ②162+164+166+…+400=2+4+6+…+400-(2+4+…+160)=200×201-80×81=33 720

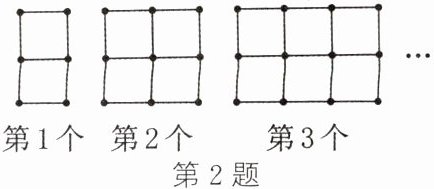
2. 如图,用火柴棒按某种规律摆成的第 1 个图案中有 2 个正方形,第 2 个图案中有 5 个正方形,第 3 个图案中有 8 个正方形,…$$,以此类推,继续摆后面的图案。
(1)第 5 个图案中有14个正方形；
(2)第$n$个图案中有(3n-1)个正方形。

答案： （1）14 （2）(3n-1)

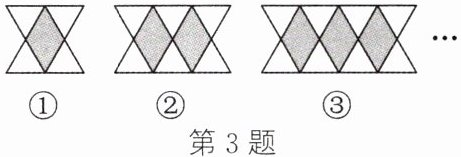
3. 用火柴棍拼成如图所示的图案,其中第①个图案由 4 个小等边三角形围成 1 个小四边形,第②个图案由 6 个小等边三角形围成 2 个小四边形,第③个图案由 8 个小等边三角形围成 3 个小四边形……$$以此类推,则第$n$个图案需要火柴棍的根数为____6n+6__(用含$n$的式子表示)。

答案： 6n+6 解析:第①个图案需要火柴棍的根数为12=3×4,第②个图案需要火柴棍的根数为18=3×6,第③个图案需要火柴棍的根数为24=3×8,…,所以第n个图案需要火柴棍的根数为3(2n+2)=6n+6.

4. 学校餐厅中,一张桌子可坐 6 人,现有以下两种摆放方式：
(1)当有 5 张桌子时,第一种方式能坐22人,第二种方式能坐14人。
(2)当有$n$张桌子时,第一种方式能坐(4n+2)人,第二种方式能坐(2n+4)人。
(3)新学期有 200 人在学校就餐,但餐厅只有 60 张这样的桌子,现在请你当一回小老师,你打算选择哪种方式来摆放桌子？为什么？
选择第一种方式.第一种方式:60张桌子一共可以坐60×4+2=242(人).第二种方式:60张桌子一共可以坐60×2+4=124(人).因为242＞200＞124,所以选择第一种方式

答案： （1）22 14 （2）(4n+2) (2n+4) （3）选择第一种方式.第一种方式:60张桌子一共可以坐60×4+2=242(人).第二种方式:60张桌子一共可以坐60×2+4=124(人).因为242＞200＞124,所以选择第一种方式