《2025年通城学典课时作业本七年级数学上册湘教版》

19. (新考法·新定义题)用“※”定义一种新运算：对于任何有理数a和b,规定$a※b = ab + b^2$。如$1※2 = 1×2 + 2^2 = 6$,则$(-4)※2$的值为(A)
A.-4
B.8
C.4
D.-8

答案： A

20. (2024·娄底涟源段考)$3\frac{1}{3}的相反数与-2\frac{2}{3}$的绝对值的和为$-\dfrac{2}{3}$。

答案： $-\dfrac{2}{3}$

21. (新考法·探究题)一个长方形的面积为$96000000 cm^2$,第一次截去它的$\frac{1}{2}$,第二次截去剩下的$\frac{1}{2}$……如此截下去,第六次截去后剩余图形的面积为1500000$cm^2$,用科学记数法表示剩余图形的面积为$1.5× 10^{6}$$cm^2$。

答案： 1500000 $1.5× 10^{6}$

22. (2024·长沙宁乡期末)如图,根据给出的数轴及已知条件,解答下列问题：
(1)A,B两点之间的距离为4；
(2)到点B的距离为3的点表示的数是1或-5；
(3)已知在数轴上点M表示的数是m,点M向左移动6个单位长度,此时点M表示的数和m互为相反数,求出m的值；
(4)若将数轴折叠,使得点A与点C重合,求与点B重合的点表示的数。
]

答案： （1）4（2）1或$-5$（3）因为在数轴上点M表示的数是m,点M向左移动6个单位长度,所以此时点M表示的数为$m-6$.因为此时点M表示的数和m互为相反数,所以$m+m-6=0$.所以$m=3$（4）因为点A表示的数为2,点C表示的数为$-3$,将数轴折叠,使得点A与点C重合,所以折叠点表示的数为$\dfrac{2+(-3)}{2}=-\dfrac{1}{2}$.所以与点B重合的点表示的数为$-\dfrac{1}{2}+\left \lbrack -\dfrac{1}{2}-(-2)\right\rbrack=1$

23. (新情境·游戏活动)有一个填写运算符号的游戏：在“$1$______$(3$______$4)$______$(-2)^2$______$10$”中的每条横线上,填入运算符号+,-,×,÷中的某一个(可重复使用),然后计算结果。
(1)计算：$1 ÷ (3 - 4) + (-2)^2 - 10$；
(2)嘉嘉填入符号后得到的算式为$1 × (3 ÷ 4) - (-2)^2$______$10$,一不小心擦掉了横线上的一个运算符号,但她知道结果是$\frac{7}{20}$,请添加符号后写出计算过程；
(3)若在横线上填入运算符号后,使计算结果最小,则这个最小结果为______。
(1)$1÷(3-4)+(-2)^{2}-10=1÷(-1)+4-10=-1+4-10=-7$
(2)$1×(3÷4)-(-2)^{2}÷10=1×\dfrac{3}{4}-4÷10=\dfrac{3}{4}-\dfrac{2}{5}=\dfrac{15}{20}-\dfrac{8}{20}=\dfrac{7}{20}$
(3)$-479$

答案： （1）$1÷(3-4)+(-2)^{2}-10=1÷(-1)+4-10=-1+4-10=-7$（2）$1×(3÷4)-(-2)^{2}÷10=1×\dfrac{3}{4}-4÷10=\dfrac{3}{4}-\dfrac{2}{5}=\dfrac{15}{20}-\dfrac{8}{20}=\dfrac{7}{20}$（3）$-479$

24. (新情境·日常生产)某冷库一天的冷冻食品进出记录如下表(运进用正数表示,运出用负数表示)：

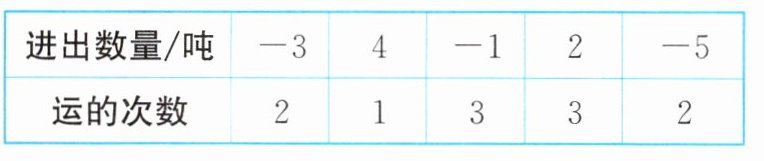
(1)这天冷库的冷冻食品比原来增加了还是减少了？增加或减少了多少吨？
(2)根据实际情况,现有两种方案：
方案一：运进每吨冷冻食品的费用是500元,运出每吨冷冻食品的费用是800元；
方案二：不管是运进还是运出,每吨冷冻食品的费用都是600元。
从节约运费的角度考虑,选用哪一种方案比较合适？

答案： （1）$(-3)×2+4×1+(-1)×3+2×3+(-5)×2=-6+4-3+6-10=-9$(吨).所以这天冷库的冷冻食品比原来减少了,减少了9吨（2）方案一总费用:$500×(4×1+2×3)+800×(|-3|×2+|-1|×3+|-5|×2)=500×10+800×19=5000+15200=20200$(元),方案二总费用:$600×(|-3|×2+4×1+|-1|×3+2×3+|-5|×2)=600×29=17400$(元).因为$20200＞17400$,所以选用方案二比较合适