《2025年通城学典课时作业本七年级数学上册湘教版》

8. 要使算式$-3^{4}◯[2^{3}-(-2)^{3}]$的计算结果最大,在“$◯$”里填入的运算符号应是(D)
A.$+$
B.$-$
C.$×$
D.$÷$

答案： D

9. 计算$(-3)^{3}÷2\frac{1}{4}×\left(-\frac{2}{3}\right)^{2}+4-2^{2}×\left(-\frac{1}{3}\right)$的结果是(A)
A.$0$
B.$1$
C.$2$
D.$3$

答案： A

10. 计算：$2.1×10^{4}-8.6×10^{3}= $$1.24×10^{4}$(结果用科学记数法表示).

答案： 1.24×10⁴

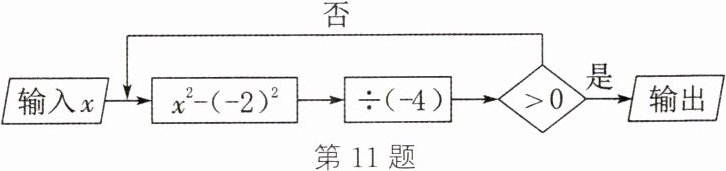
11. 如图所示为一个简单的数值计算程序,若输入$x的值为2$,则输出的结果为1.
]

答案： 1 解析：若输入x的值为2，则有[2²-(-2)²]÷(-4)=0.因为0=0，所以再输入0，则有[0²-(-2)²]÷(-4)=1.因为1＞0，所以输出的结果为1.

12. 计算：
(1)($2024·$常德期末)$(-1)^{4}-\left(1-\frac{1}{2}\right)÷(-2)×[3-(-3)^{2}]$；
(2)$(-2)^{2}-\vert -3 + 2\vert+\left(\frac{1}{6}-1\frac{2}{3}+\frac{1}{2}\right)÷\left(-\frac{1}{12}\right)$.

答案： （1）原式=1-$\frac{1}{2}$÷(-2)×(-6)=1-$\frac{3}{2}$=-$\frac{1}{2}$
（2）原式=4-1+($\frac{1}{6}$-$\frac{5}{3}$+$\frac{1}{2}$)×(-12)=4-1+$\frac{1}{6}$×(-12)-$\frac{5}{3}$×(-12)+$\frac{1}{2}$×(-12)=4-1+(-2)+20+(-6)=15

13. 小明做了如下一道有理数混合运算的题目：
$-3^{4}÷(-27)-\left[(-2)×\left(-\frac{4}{3}\right)+(-2)\right]^{3}$
$=81÷(-27)-\left[\frac{8}{3}+(-8)\right]$
…$=$
(1)请用圆圈圈出小明第一步计算中的错误；
(2)请写出这道题正确的解答过程.

答案： （1）-3⁴÷(-27)-[(-2)×(-$\frac{4}{3}$)+(-2)]³=81÷(-27)-[$\frac{8}{3}$+(-8)]³=… （2）-3⁴÷(-27)-[(-2)×(-$\frac{4}{3}$)+(-2)]³=-81÷(-27)-($\frac{8}{3}$-2)³=81×$\frac{1}{27}$-($\frac{2}{3}$)³=3-$\frac{8}{27}$=2$\frac{19}{27}$

14. 学习了有理数后,为练习加、减、乘、除以及乘方混合运算,智慧学习小组自制了一副卡片,每张卡片上分别标有从$-13至13$的其中一个整数(不含$0$),每个整数有$2$张相同的卡片,共$52$张.每天课余,小组成员会做五分钟的混合运算游戏.每次随机抽取$4$张卡片,根据卡片上的数进行混合运算(每张卡片必须用一次且只能用一次,可以加括号),使得运算结果为$24或-24$.例如随机抽取的$4张卡片上的数分别为1$,$-2$,$2$,$3$,可以列式为$2^{3}×(-2 - 1)= 8×(-3)= -24$.如果随机抽取的$4张卡片上的数分别为2$,$-2$,$5$,$-1$,请列出计算结果为$24或-24$的两个不同的算式.

答案： 答案不唯一，如[2-(-2)]×[5-(-1)]=24，2×(-2)×(-1-5)=24