《2025年通城学典课时作业本七年级数学上册湘教版》

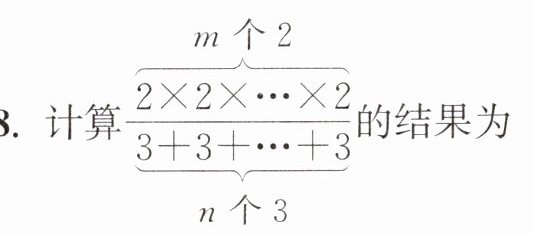
8. 计算$\frac{\overbrace{2×2×…×2}^{m个2}}{\underbrace{3+3+…+3}_{n个3}}$的结果为(B)

A.$\frac{2m}{3^{n}}$
B.$\frac{2^{m}}{3n}$
C.$\frac{2m}{n^{3}}$
D.$\frac{m^{2}}{3n}$

答案： B

9. 若$|a+\frac{1}{2}|+(b-3)^{2}= 0$,则$a^{b}$的值为(A)
A.$-\frac{1}{8}$
B.$\frac{1}{8}$
C.$-\frac{3}{2}$
D.$-8$

答案： A

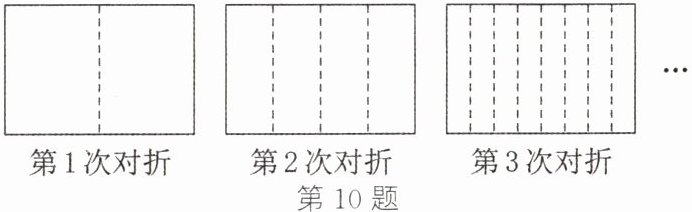
10. 如图,将一张长方形纸对折 1 次,可以得到 1 条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折 3 次后,可以得到 7 条折痕……以此类推,对折 2026 次,可以得到折痕的条数为(D)


A.2025
B.2026
C.$2^{2025}-1$
D.$2^{2026}-1$

答案： D 解析:由题图,可知第1次对折,把长方形纸分成2个部分,有1条折痕;第2次对折,把长方形纸分成4个部分,有3条折痕;第3次对折,把长方形纸分成8个部分,有7条折痕……以此类推,第2026次对折,把长方形纸分成$2^{2026}$个部分,有$(2^{2026}-1)$条折痕.

11. 若$a^{2}= 4$,$b^{3}= 27$,且$a\cdot b＜0$,则$a + b = $1.

答案： 1

12. 平方等于 9 的数是$\pm3$,立方等于 8 的数是2,平方等于它本身的数是0,1,立方等于它本身的数是0,$\pm1$.

答案： $\pm3$ 2 0,1 0,$\pm1$

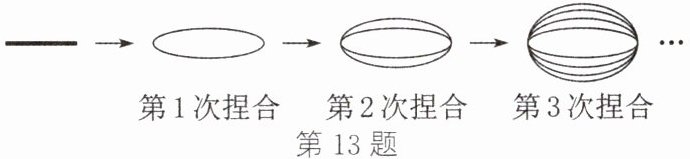
13. (新情境·日常生活)如图,拉面馆的师傅用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条.照这样,第 6 次捏合后可拉出几根面条？

答案： 根据题意,得$2^6=64$(根),所以第6次捏合后可拉出64根面条

14. 已知$|a| = 3$,$|b| = 2$,且$a ＜ b$,求$(a + b)^{3}$的值.

答案： 因为$|a|=3$,所以$a=\pm3$.因为$|b|=2$,所以$b=\pm2$.又因为$a\lt b$,所以$a=-3$,$b=\pm2$.当$a=-3$,$b=2$时,$(a+b)^3=(-3+2)^3=-1$;当$a=-3$,$b=-2$时,$(a+b)^3=(-3-2)^3=(-5)^3=-125$

15. (新考法·探究题)观察下列各式：
$1^{3}+2^{3}= 9= \frac{1}{4}×4×9= \frac{1}{4}×2^{2}×3^{2}$；
$1^{3}+2^{3}+3^{3}= 36= \frac{1}{4}×9×16= \frac{1}{4}×3^{2}×4^{2}$；
$1^{3}+2^{3}+3^{3}+4^{3}= 100= \frac{1}{4}×16×25= \frac{1}{4}×4^{2}×5^{2}$；
…
(1)计算$1^{3}+2^{3}+3^{3}+4^{3}+…+10^{3}$的值；
(2)试猜想$1^{3}+2^{3}+3^{3}+4^{3}+…+n^{3}$的值.

答案：
(1)$1^3+2^3+3^3+4^3+\cdots+10^3=\frac{1}{4}×10^2×(10+1)^2=\frac{1}{4}×100×121=3025$；
(2)$1^3+2^3+3^3+4^3+\cdots+n^3=\frac{1}{4}n^2(n+1)^2$