《2025年通城学典课时作业本七年级数学上册湘教版》

8. 有下列计算：①$24+(-18)+6+(-12)= [(-18)+(-12)]+(24+6)$；②$(-\frac{1}{2})+1+(-\frac{1}{4})+\frac{1}{3}= [(-\frac{1}{2})+(-\frac{1}{4})]+(1+\frac{1}{3})$；③$(-0.5)+3\frac{3}{4}+3.25+(-5\frac{1}{2})= [(-0.5)+(-5\frac{1}{2})]+(3\frac{3}{4}+3.25)$.其中正确运用加法运算律的有(D)
A.$0$个
B.$1$个
C.$2$个
D.$3$个

答案： D

9. 已知$A地的海拔为3.72$米,现在测量$B$,$C$,$D$,$E$,$F$五地的海拔,每次测量的结果如下表(单位：米)：

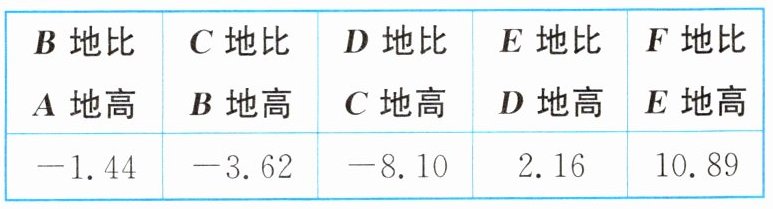
问$F$地的海拔是多少？

答案： 3.72+(-1.44)+(-3.62)+(-8.10)+2.16+10.89=(3.72+2.16+10.89)+[(-1.44)+(-3.62)+(-8.10)]=3.61(米)，所以F地的海拔是3.61米

10. (易错题)阅读下题的计算方法：
计算：$(-5\frac{5}{6})+(-9\frac{2}{3})+17\frac{3}{4}+(-3\frac{1}{2})$.
解：原式$=[(-5)+(-\frac{5}{6})]+[(-9)+(-\frac{2}{3})]+(17+\frac{3}{4})+[(-3)+(-\frac{1}{2})]= [(-5)+(-9)+17+(-3)]+[(-\frac{5}{6})+(-\frac{2}{3})+\frac{3}{4}+(-\frac{1}{2})]= 0+(-\frac{5}{4})= -\frac{5}{4}$.
上面这种计算方法叫作拆分法,请按此方法计算：$(-55\frac{3}{4})+(-44\frac{2}{3})+100\frac{2}{3}+(-1\frac{1}{4})$.

答案： 原式=[(-55)+(-$\frac{3}{4}$)]+[(-44)+(-$\frac{2}{3}$)]+(100+$\frac{2}{3}$)+[(-1)+(-$\frac{1}{4}$)]=[(-55)+(-44)+100+(-1)]+[(-$\frac{3}{4}$)+(-$\frac{2}{3}$)+$\frac{2}{3}$+(-$\frac{1}{4}$)]=0+(-1)=-1
[易错分析]运用“拆分法”对带分数进行拆分时，分开的整数部分与分数部分必须保留原带分数的符号，如-55$\frac{3}{4}$应拆分为(-55)+(-$\frac{3}{4}$)，而非(-55)+$\frac{3}{4}$.

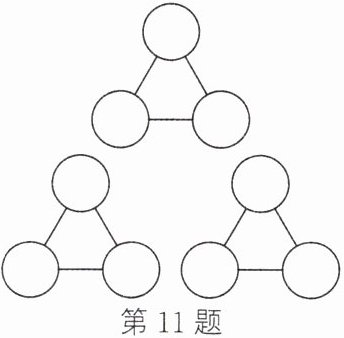
11. (新考向·代数推理)如图所示为三个三角形,每个三角形的顶点处都有一个“$◯$”,按要求在每个“$◯$”中填入一个数.
(1)将$-8$,$-7$,$-6$,$-4$,$1$,$3$,$5$,$9$,$13$这九个数填入恰当的位置,使得每个三角形的三个顶点处的“$◯$”中的数的和都等于$2$.
(2)如果将(1)中的这九个数改为$-13$,$-9$,$-5$,$-3$,$-1$,$4$,$6$,$7$,$8$,还能满足上述要求吗？如果能满足,请填在“$◯$”中；如果不能满足,请说明理由.

答案：

(1)如图所示
(2)不能 理由：(-13)+(-9)+(-5)+(-3)+(-1)+4+6+7+8=(-31)+25=-6，如果每个三角形的三个顶点处的“○”中的数的和都等于2，那么这九个数的和为6.因为-6≠6，所以如果将
(1)中的这九个数改为-13，-9，-5，-3，-1，4，6，7，8，不能满足要求.