《2025年通城学典课时作业本七年级数学上册湘教版》

5. (新考向·代数推理)某次知识竞赛有20道必答题,每答对1道题得10分,答错或不答都扣5分;3道抢答题,每道题抢答对得10分,抢答错扣20分,抢答不到不得分也不扣分.甲、乙两队进入决赛,甲队必答题得了170分,乙队必答题答错或不答的有1道.
(1)甲队必答题答对的、答错或不答的分别有多少道?
(2)抢答赛中,乙队抢答对了第1题,又抢到了第2题,但还没作答时,甲队啦啦队队员小黄说:“我们甲队输了!”小汪说:“你的判断不一定对!”请你举一例说明小黄的判断为何不一定对.

答案： （1）设甲队必答题答对的、答错或不答的分别有x道，y道. 根据题意，得$\left\{\begin{array}{l} 10x-5y=170,\\ x+y=20,\end{array}\right. $解得$\left\{\begin{array}{l} x=18,\\ y=2.\end{array}\right. $所以甲队必答题答对的、答错或不答的分别有18道，2道 （2）举例不唯一，如甲队现在得分为170分，则乙队现在得分为$19×10-5+10=195$(分). 若第2题乙队抢答错误，第3题甲队抢答正确，则乙队最后得分为$195-20=175$(分)，甲队最后得分为$170+10=180$(分). 因为$175＜180$，所以甲队获胜. 所以小黄的判断不一定对

6. (新考向·代数推理)在某学校组织的竞赛活动中,为奖励成绩优秀的同学,某班班长代表学校购买了一些学习用品,他与学习委员的对话如图所示.

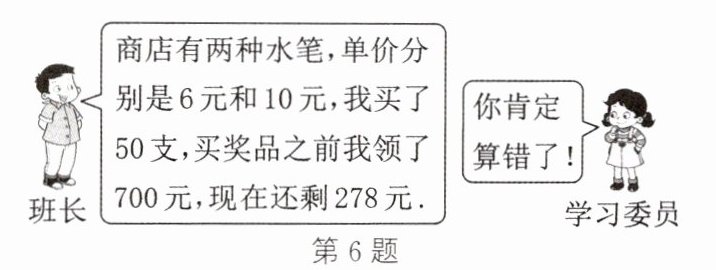
(1)请根据图中信息,列出二元一次方程组,并通过求解说明班长确实算错了;
(2)若要领来的700元全部用来买水笔,恰好花完,班长用列表法将所用方案进行了梳理:

则满足条件的所有方案共有24种,表中a+b的最大值是116.
（1）设购买单价为6元的水笔x支，单价为10元的水笔y支. 根据题意，得$\left\{\begin{array}{l} x+y=50,\\ 6x+10y=700-278,\end{array}\right. $解得$\left\{\begin{array}{l} x=19.5,\\ y=30.5.\end{array}\right. $因为x，y为整数，所以班长确实算错了

答案： （1）设购买单价为6元的水笔x支，单价为10元的水笔y支. 根据题意，得$\left\{\begin{array}{l} x+y=50,\\ 6x+10y=700-278,\end{array}\right. $解得$\left\{\begin{array}{l} x=19.5,\\ y=30.5.\end{array}\right. $因为x，y为整数，所以班长确实算错了 （2）24 116 解析：根据题意，得$6a+10b=700$. 所以$a=\frac {700-10b}{6}$. 所以$a+b=\frac {700-10b}{6}+b=\frac {700-4b}{6}$. 令$y=a+b=\frac {700-4b}{6}$，所以y的值随着b值的增大而减小. 因为$6a+10b=700$，a，b均为非负整数，所以$\left\{\begin{array}{l} a=0,\\ b=70,\end{array}\right. \left\{\begin{array}{l} a=5,\\ b=67,\end{array}\right. ... ,\left\{\begin{array}{l} a=115,\\ b=1.\end{array}\right. $因为$115=5×23$，所以a取值的个数为$23+1=24$. 当$b=1$时，y取得最大值，此时$y=116$. 综上所述，满足条件的所有方案共有24种，表中$a+b$的最大值是116.

7. (新情境·日常生产)已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.

答案： （1）设每辆A型车、B型车都载满货物一次可以分别运货x吨、y吨. 依题意，得$\left\{\begin{array}{l} 2x+y=10,\\ x+2y=11,\end{array}\right. $解方程组，得$\left\{\begin{array}{l} x=3,\\ y=4.\end{array}\right. $所以1辆A型车载满货物一次可运货3吨，1辆B型车载满货物一次可运货4吨 （2）结合题意和（1），得$3a+4b=31$，所以$a=\frac {31-4b}{3}$. 因为a，b都是正整数，所以$\left\{\begin{array}{l} a=9,\\ b=1\end{array}\right. $或$\left\{\begin{array}{l} a=5,\\ b=4\end{array}\right. $或$\left\{\begin{array}{l} a=1,\\ b=7.\end{array}\right. $所以有3种租车方案：方案一：租A型车9辆，B型车1辆；方案二：租A型车5辆，B型车4辆；方案三：租A型车1辆，B型车7辆 （3）因为A型车每辆需租金100元/次，B型车每辆需租金120元/次，所以方案一需租金$9×100+1×120=1020$(元)；方案二需租金$5×100+4×120=980$(元)；方案三需租金$1×100+7×120=940$(元). 因为$1020＞980＞940$，所以最省钱的租车方案是方案三：租A型车1辆，B型车7辆，最少租车费为940元