第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. (甘肃武威期中)甲、乙两物体比热容之比为 $2:3$,质量之比为 $1:3$,若两者吸收热量之比为 $2:5$,则甲、乙两物体升高的温度之比为 (
A.$5:9$
B.$4:3$
C.$9:5$
D.$3:5$
C
)A.$5:9$
B.$4:3$
C.$9:5$
D.$3:5$
答案:
1.C[由$Q_{吸}=cm\Delta t$可知,甲、乙两物体升高的温度之比:$\frac{\Delta t_{甲}}{\Delta t_{乙}}=$$\frac{\frac{Q_{甲}}{c_{甲}m_{甲}}}{\frac{Q_{乙}}{c_{乙}m_{乙}}}=\frac{Q_{甲}}{Q_{乙}}×\frac{c_{乙}m_{乙}}{c_{甲}m_{甲}}=\frac{2}{2×1}×\frac{3×3}{5}=\frac{9}{5}$,故C正确,ABD错误。]
2. (天津滨海新区校级期中)质量之比为 $2:3$ 的甲、乙两种液体,当它们吸收的热量之比为 $7:5$ 时,升高的温度之比为 $6:5$,则甲、乙的比热容之比为
7∶4
,若把甲、乙两种液体各倒掉一半,剩下液体比热容之比为7∶4
。
答案:
2.7∶4 7∶4
3. (河北保定期中)已知铜、铅的比热容之比为 $3:1$。有一块铜和一块铅的质量之比为 $4:5$,若它们升高相同的温度,则铜、铅吸收的热量之比为
12∶5
;若它们吸收相同的热量,则铜、铅升高的温度之比为5∶12
。
答案:
3.12∶5 5∶12[若它们升高相同的温度,由$Q_{吸}=cm\Delta t$可知,铜、铅吸收的热量之比为$\frac{Q_{吸铜}}{Q_{吸铅}}=\frac{c_{铜}m_{铜}\Delta t}{c_{铅}m_{铅}\Delta t}=\frac{3×4×1}{1×5×1}=\frac{12}{5}$;若它们吸收相同的热量,由$\Delta t=\frac{Q_{吸}}{cm}$可知,铜、铅升高的温度之比为$\frac{\Delta t_{铜}}{\Delta t_{铅}}=$$\frac{\frac{Q_{吸铜}}{c_{铜}m_{铜}}}{\frac{Q_{吸铅}}{c_{铅}m_{铅}}}=\frac{Q_{吸铜}}{Q_{吸铅}}×\frac{c_{铅}m_{铅}}{c_{铜}m_{铜}}=\frac{Q_{吸铜}c_{铅}m_{铅}}{Q_{吸铅}c_{铜}m_{铜}}=\frac{1×1×5}{1×3×4}=\frac{5}{12}$。]
4. 用相同的电加热器分别对质量相等的 $A$ 和 $B$ 两种液体(不计热量损失)加热,如图所示是 $A$ 和 $B$ 的温度随加热时间变化的图像。下列说法正确的是 (
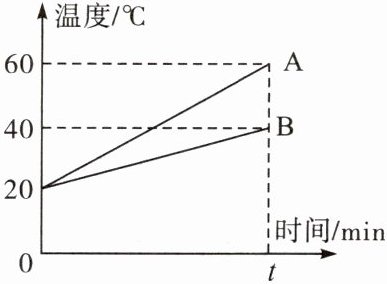
A.$A$ 与 $B$ 的比热容之比为 $2:1$
B.$A$ 与 $B$ 的比热容之比为 $2:3$
C.都加热 $t$ 时间,$B$ 吸收热量多
D.$A$ 和 $B$ 升高相同的温度,$B$ 吸收的热量多
D
)
A.$A$ 与 $B$ 的比热容之比为 $2:1$
B.$A$ 与 $B$ 的比热容之比为 $2:3$
C.都加热 $t$ 时间,$B$ 吸收热量多
D.$A$ 和 $B$ 升高相同的温度,$B$ 吸收的热量多
答案:
4.D[由于A、B两种液体质量相等,初温相同,用相同的加热器加热相同的时间t min,表示A、B吸收的热量相同,A温度升高了$\Delta t_{A}=60^{\circ}C-20^{\circ}C=40^{\circ}C$,B温度升高了$\Delta t_{B}=40^{\circ}C-$$20^{\circ}C=20^{\circ}C$,$m_{A}:m_{B}=1:1$,$Q_{A}:Q_{B}=1:1$,$\Delta t_{A}:\Delta t_{B}=$$40^{\circ}C:20^{\circ}C=2:1$,根据$Q_{吸}=cm\Delta t$可得,A与B的比热容之比$c_{A}:c_{B}=\frac{Q_{A}}{m\Delta t_{A}}:\frac{Q_{B}}{m\Delta t_{B}}=\frac{Q_{A}}{Q_{B}}×\frac{m\Delta t_{B}}{m\Delta t_{A}}=\frac{1}{1}×\frac{1}{2}=1:2$,故AB错误;用相同的加热器加热相同的时间t min,表示A、B吸收的热量相同,故C错误;由于A、B两种液体质量相等,初温相同,当A、B升高相同的温度,B的比热容大,吸收的热量$Q_{吸B}=$$c_{B}m_{B}\Delta t_{B}$,则A和B升高相同的温度,B吸收热量较多,故D正确。]
5. (安徽蚌埠二模)将一杯热水倒入盛有一些冷水的容器中,冷水的温度升高了 $20^{\circ}C$,又向容器内倒入同样一杯热水,冷水温度又升高了 $10^{\circ}C$,如果再向容器内倒入同样一杯热水,则冷水温度可再升高(不计热损失,热水和冷水的比热容相同) (
A.$8^{\circ}C$
B.$7^{\circ}C$
C.$6^{\circ}C$
D.$5^{\circ}C$
C
)A.$8^{\circ}C$
B.$7^{\circ}C$
C.$6^{\circ}C$
D.$5^{\circ}C$
答案:
5.C
6. (河北沧州校级月考)网上曾热销一种“55 度杯”,称“能很快将开水变成适饮的温水,而后又能将凉水变成适饮的温水”。为破解此中秘密,物理小组设计如图模型,设此模型内胆中封存着 $300g$ 水,室温 $20^{\circ}C$;现向杯中倒入 $200g$、$100^{\circ}C$ 开水,摇一摇,热平衡后杯内水温迅速降至 $t_{1}=$

52
$^{\circ}C$;然后将杯内水倒掉,迅速将 $200g$ 室温某液态物质倒入该杯,摇一摇,这种液态物质的温度可升至 $44^{\circ}C$,则这种液态物质的比热容为$2.1×10^{3}$
$J/(kg\cdot ^{\circ}C)$ $[c_{水}= 4.2× 10^{3}J/(kg\cdot ^{\circ}C)$,忽略整个过程中内胆及空间的热损失$]$。
答案:
6.52 $2.1×10^{3}$[热水放出的热量为$Q_{放}=c_{水}m_{1}(t_{0}-t_{1})$,冷水吸收的热量为$Q_{吸}=c_{水}m_{2}(t_{1}-t_{0}')$,假设热水放出的热量全部被凉水吸收,则$Q_{吸}=Q_{放}$,即$4.2×10^{3}\ J/(kg·^{\circ}C)×0.2\ kg×$$(100^{\circ}C-t_{1})=4.2×10^{3}\ J/(kg·^{\circ}C)×0.3\ kg×(t_{1}-20^{\circ}C)$,解得$t_{1}=52^{\circ}C$;放入液体后,水降低的温度$\Delta t'=52^{\circ}C-44^{\circ}C=$$8^{\circ}C$,水放出的热量为$Q_{放}'=c_{水}m_{2}\Delta t'=4.2×10^{3}\ J/(kg·^{\circ}C)×$$0.3\ kg×8^{\circ}C=1.008×10^{4}\ J$,液体吸收的热量$Q_{吸液}'=Q_{放}'=$$1.008×10^{4}\ J$,液体升高的温度为$\Delta t''=44^{\circ}C-20^{\circ}C=24^{\circ}C$,由$Q_{吸}=cm\Delta t$得,液体的比热容为$c_{液}=\frac{Q_{吸液}'}{m_{液}\Delta t''}=\frac{1.008×10^{4}\ J}{0.2\ kg×24^{\circ}C}=$$2.1×10^{3}\ J/(kg·^{\circ}C)$。]
7. 一个质量为 $0.5kg$ 的铝壶里面装有 $5kg$、$20^{\circ}C$ 的水,现将它们一起加热,吸收热量后它们的温度升高了 $50^{\circ}C$。则:
(1)铝壶吸收了多少热量?
(2)水吸收了多少热量?
(3)若它们共同吸收的热量由 $100^{\circ}C$ 的水,降温到 $50^{\circ}C$ 提供,则需要 $100^{\circ}C$ 的水多少 $kg$?$[c_{铝}= 0.88× 10^{3}J/(kg\cdot ^{\circ}C)$,$c_{水}= 4.2× 10^{3}J/kg\cdot ^{\circ}C]$
(1)铝壶吸收了多少热量?
(2)水吸收了多少热量?
(3)若它们共同吸收的热量由 $100^{\circ}C$ 的水,降温到 $50^{\circ}C$ 提供,则需要 $100^{\circ}C$ 的水多少 $kg$?$[c_{铝}= 0.88× 10^{3}J/(kg\cdot ^{\circ}C)$,$c_{水}= 4.2× 10^{3}J/kg\cdot ^{\circ}C]$
答案:
7.解:(1)铝壶吸收的热量$Q_{铝吸}=c_{铝}m_{铝}\Delta t_{铝}=0.88×$$10^{3}\ J/(kg·^{\circ}C)×0.5\ kg×50^{\circ}C=2.2×10^{4}\ J$;(2)水吸收的热量$Q_{水吸}=c_{水}m_{水}\Delta t_{水}=4.2×10^{3}\ J/(kg·^{\circ}C)×$$5\ kg×50^{\circ}C=1.05×10^{6}\ J$;(3)根据题意,热水放出的热量$Q_{放}=Q_{铝吸}+Q_{水吸}=2.2×10^{4}\ J+$$1.05×10^{6}\ J=1.072×10^{6}\ J$,根据$Q=cm\Delta t$,所需热水的质量$m_{热水}=\frac{Q_{放}}{c_{水}\Delta t_{热水}}=\frac{1.072×10^{6}\ J}{4.2×10^{3}\ J/(kg·^{\circ}C)×(100^{\circ}C-50^{\circ}C)}\approx$$5.1\ kg$。
查看更多完整答案,请扫码查看


