第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
5. 已知 $ (x - 3)^2 + |y + 4| = 0 $,则代数式 $ (x + y)^{520} $ 的值为 (
A.$ 1 $
B.$ -1 $
C.$ \pm 1 $
D.$ 2024 $
1
)A.$ 1 $
B.$ -1 $
C.$ \pm 1 $
D.$ 2024 $
答案:
A 解析 因为(x-3)²+|y+4|=0,所以(x-3)²=0,|y+4|=0,所以x=3,y=-4. 所以(x+y)⁵²⁰=(3-4)⁵²⁰=(-1)⁵²⁰=1.
观察下列“蜂窝图”,按照这样的规律,则第 678 个图案中的 的个数是 (
的个数是 (
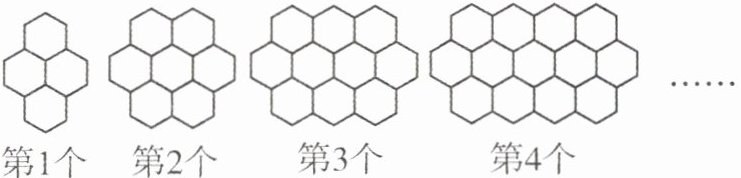
A.$ 2039 $
B.$ 2037 $
C.$ 2035 $
D.$ 2033 $
 的个数是 (
的个数是 (C
)
A.$ 2039 $
B.$ 2037 $
C.$ 2035 $
D.$ 2033 $
答案:
解析 因为第 1 个图案中的“$ ◯ $”的个数为 $ 3 × 1 + 1 = 4 $(个). 第 2 个图案中的“$ ◯ $”的个数为 $ 3 × 2 + 1 = 7 $(个). 第 3 个图案中的“$ ◯ $”的个数为 $ 3 × 3 + 1 = 10 $(个). 所以第 $ n $ 个图案中的“$ ◯ $”的个数为 $ (3n + 1) $ 个. 第 678 个图案中的“$ ◯ $”的个数为 $ 3 × 678 + 1 = 2035 $(个).
答案 C
答案 C
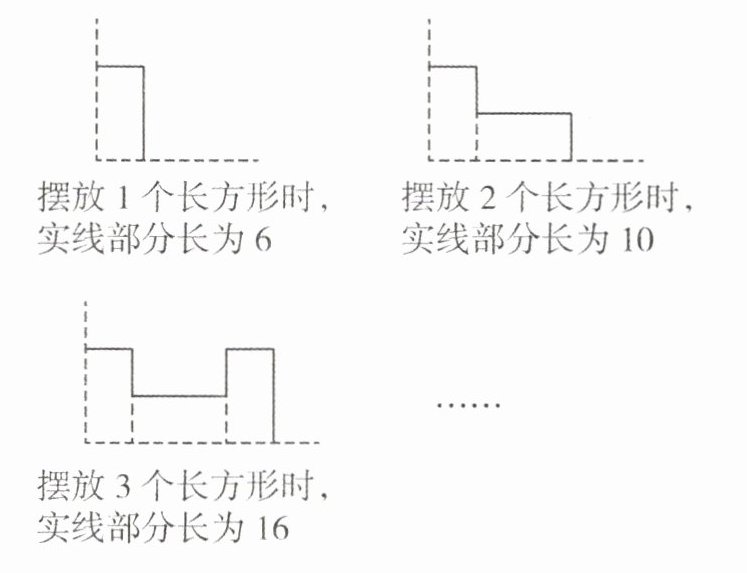
6. 将相同的长方形卡片摆放在一个直角上,摆放方式如图所示,每个长方形卡片长为 $ 4 $、宽为 $ 2 $,依此类推,摆放 $ 123 $ 个长方形时,实线部分长为
616
.
答案:
616 解析 第1个图实线部分长为6,第2个图实线部分长为6+4,第3个图实线部分长为6+4+6,第4个图实线部分长为6+4+6+4,第5个图实线部分长为6+4+6+4+6,第6个图实线部分长为6+4+6+4+6+4,……从上述规律可以看到,对于第n个图形,当n为奇数时,第n个图形实线部分长为$\frac{1}{2}×(6+4)(n-1)+6$. 当n为偶数时,第n个图形实线部分长为$\frac{1}{2}(6+4)n$,所以摆放123个长方形时,实线部分长为$\frac{1}{2}×(6+4)×(123-1)+6=616$.
规定一种运算,运算法则是 $ a * b = 2a - b $,求 $ 4 * 3 $ 的值.
答案:
解 由定义知,$ 4 * 3 = 2 × 4 - 3 = 5 $.
7. 规定一种运算,运算法则是 $ x | y = |(x - 8) \cdot y| $. 当 $ x = 5 $,$ y = 3 $ 时,求 $ x | y $ 的值.
答案:
解 当x=5,y=3时,x|y=5|3|=(5-8)×3|=|-3×3|=9.
查看更多完整答案,请扫码查看


